
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
【尝试】
(1)当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
【发现】
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
【应用】
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.

【答案】【尝试】(1)(1,﹣2).(2)点A(2,0)在抛物线l上.(3)6.【发现】抛物线l必过定点(2,0)、(﹣1,6).【应用1】见解析
【解析】试题分析:
1、【尝试】(1)将t=2代入抛物线L中,化简,再配方,即可得到抛物线L的顶点坐标;
(2)将点A的横坐标x=2代入抛物线L的解析式中进行计算看y是否等于0,即可判断出点A是否在抛物线L上;
(3)将点B的横坐标x=-1代入抛物线L的解析式中计算出对应的y的值即可得到n的值;
2、【发现】将抛物线L的解析式展开可得: y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=t(x﹣2)(x+1)﹣2x+4,由此可得:当x=2时,y=0;当x=-1时,y=6;这就说明抛物线L总过定点A(2,0)和B(-1,6);
3、【应用】由【发现】可知,二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的“再生二次函数”必过点(2,0)和点(-1,6),因此检验这两个点是否都在二次函数y=﹣3x2+5x+2的图象上即可作出判断.
试题解析:
1、【尝试】
(1)∵将t=2代入抛物线l中,得:y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=2x2﹣4x=2(x﹣1)2﹣2,
∴此时抛物线的顶点坐标为:(1,﹣2).
(2)∵将x=2代入y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4),得 y=0,
∴点A(2,0)在抛物线l上.
(3)将x=﹣1代入抛物线l的解析式中,得:
n=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=6.
2、【发现】
∵将抛物线E的解析式展开,得:
y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=t(x﹣2)(x+1)﹣2x+4
∴抛物线l必过定点A(2,0)、B(﹣1,6).
3、【应用】
将x=2代入y=﹣3x2+5x+2,y=0,即点A在抛物线上.
将x=﹣1代入y=﹣3x2+5x+2,计算得:y=﹣6≠6,即抛物线y=﹣3x2+5x+2不经过点B,
∴二次函数y=﹣3x2+5x+2不是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
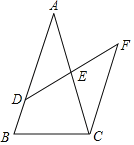
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示的数为a,点B为原点,点C表示的数为c,且已知a,c满足|a+1|+(c﹣7)2=0.
(1)a= c= ;
(2)若AC的中点为M,则点M表示的数为 ;
(3)若A,C两点同时以每秒1个单位长度的速度向左运动,求第几秒时,恰好有BA=BC?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在高速公路上的一个测速点,仪器记录下过往车辆的行驶速度(单位:千米/时),分析人员随机选取了10个速度数据如下:98,99,102,105,97,86,105,110,95,91.求这组数据的平均数、中位数和众数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 在原点
在原点![]() 的左边,表示的数为-15,点
的左边,表示的数为-15,点![]() 在原点的右边,且
在原点的右边,且![]() .点
.点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 出发向右运动.点
出发向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 出发向右运动(点
出发向右运动(点![]() ,点
,点![]() 同时出发).
同时出发).
![]()
(1)数轴上点![]() 对应的数是______,点
对应的数是______,点![]() 到点
到点![]() 的距离是______;
的距离是______;
(2)经过几秒,原点![]() 是线段
是线段![]() 的中点?
的中点?
(3)经过几秒,点![]() ,
,![]() 分别到点
分别到点![]() 的距离相等?
的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个正方体的表面涂上颜色.如图把正方体的棱![]() 等分,然后沿等分线把正方体切开,能够得到
等分,然后沿等分线把正方体切开,能够得到![]() 个小正方体,通过观察我们可以发现
个小正方体,通过观察我们可以发现![]() 个小正方体全是
个小正方体全是![]() 个面涂有颜色的.如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到
个面涂有颜色的.如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到![]() 个小正方体,通过观察我们可以发现这些小正方体中有
个小正方体,通过观察我们可以发现这些小正方体中有![]() 个是
个是![]() 个面涂有颜色的,有
个面涂有颜色的,有![]() 个是
个是![]() 个面涂有颜色的,有
个面涂有颜色的,有![]() 个是
个是![]() 个面涂有颜色的,还有
个面涂有颜色的,还有![]() 个各个面都没有涂色.
个各个面都没有涂色.

(1)如果把正方体的棱![]() 等分,所得小正方体表面涂色情况如何呢?把正方体的棱
等分,所得小正方体表面涂色情况如何呢?把正方体的棱![]() 等分呢?(请填写下表):
等分呢?(请填写下表):
棱等分数 |
|
|
| ___________个 | _____________个 |
| __________个 | ____________个 |
| ___________个 | ____________个 |
各个面都无涂色的正方体 | ___________个 | ____________个 |
(2)请直接写出将棱![]() 等分时只有一个面涂色的小正方体的个数_____________.
等分时只有一个面涂色的小正方体的个数_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空:
| 平均数(单位:年) | 众数(单位:年) | 中位数(单位:年) |
甲 | ________ | 5 | ________ |
乙 | 9.6 | ________ | 8.5 |
丙 | 9.4 | 4 | ________ |
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
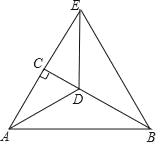
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AD平分∠CAB交BC于点D,CD=1,延长AC到E,使AE=AB,连接DE,BE.
(1)求BD的长;
(2)求证:DA=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
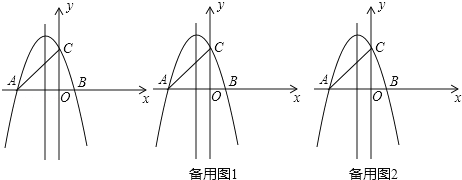
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com