练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在高速公路上的一个测速点，仪器记录下过往车辆的行驶速度(单位：千米/时)，分析人员随机选取了10个速度数据如下：98，99，102，105，97，86，105，110，95，91.求这组数据的平均数、中位数和众数．

    【答案】平均数为98.8，.中位数为98.5，众数为105

    【解析】

    求平均数只要求出数据之和再除以总个数即可;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.

    这组数据的平均数为.将这10个数据从小到大排列后，最中间两个位置上的数为98，99，∴中位数为.这10个数据中，105出现了2次，出现的次数最多，∴众数为105.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，按以下步骤作图：①分别以B、C为圆心，以大于BC的长为半径作弧，两弧相交于两点M、N；②作直线MN交AB于点D，连接CD．若∠B＝30°，∠A＝55°，则∠ACD的度数为（　　）

    A. 65°B. 60°C. 55°D. 45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设不计超市其他费用，如果超市要想至少获得20%的利润，那么这种水果的售价在进价的基础上应至少提高【 】

    A．40% B．33.4% C．33.3% D．30%

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某服装厂现有甲种布料50米，乙种布料27米，现计划用这两种布料生产A，B两种型号的时装共60套. 已知做一套A型号的时装需用甲种布料1米，乙种布料0.2米，可获利30元；做一套B型号的时装需用甲种布料0.5米，乙种布料0.8米，可获利20元. 设生产A型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元.

    （1）求y（元）与x（套）之间的函数表达式，并求出自变量的取值范围.

    （2）当生产A型号的时装多少套时，能使该厂所获利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知点是线段上一点，点在线段上，点在线段上，、两点分别从、出发以、的速度沿直线向左运动，运动方向如箭头所示．

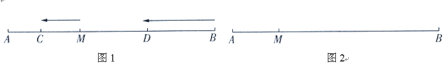
    （1）若，当点、运动了，求的值．

    （2）若点、运动时，总有，则：____________，并说明理由．

    （3）如图2，若，点是直线上一点，且，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算）

    （1） （2）

    （3） （4）

    （5） （6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4，把y=t（x2﹣3x+2）+（1﹣t）（﹣2x+4）称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线L．现有点A（2，0）和抛物线L上的点B（﹣1，n），请完成下列任务：

    【尝试】

    （1）当t=2时，抛物线y=t（x2﹣3x+2）+（1﹣t）（﹣2x+4）的顶点坐标为　 　；

    （2）判断点A是否在抛物线L上；

    （3）求n的值；

    【发现】

    通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线L总过定点，坐标为　 　．

    【应用】

    二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：数a，b，c 在数轴上的对应点如下图所示，

    （1）在数轴上表示﹣a；

    （2）比较大小（填“＜”或“＞”或“＝”）：a+b　 0，﹣3c　 0，c﹣a　 0；

    （3）化简|a+b|﹣|﹣3c|﹣|c﹣a|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

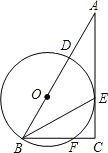
    【题目】在Rt△ABC中，∠ACB=90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC于点F．

    （1）求证：AC是⊙O的切线；

    （2）若BF=6，⊙O的半径为5，求CE的长．

    查看答案和解析>>

    同步练习册答案