
【题目】如图1,抛物线y=ax2+bx﹣3经过点A,B,C,已知点A(﹣1,0),点B(3,0)
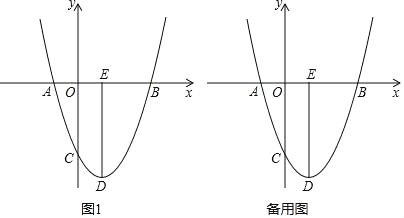
(1)求抛物线的解析式
(2)点D为抛物线的顶点,DE⊥x轴于点E,点N是线段DE上一动点
①当点N在何处时,△CAN的周长最小?
②若点M(m,0)是x轴上一个动点,且∠MNC=90°,求m的取值范围.
【答案】(1)y=x2﹣2x﹣3;(2)①N(1,﹣2);②﹣![]() ≤m≤5.
≤m≤5.
【解析】
(1)函数的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),即可求解;
(2)①过点C作x轴的平行线交抛物线于点C'(2,﹣3),连接AC'交DE于点N,则此时△CAN的周长最小,即可求解;
②如图2,ME=﹣n2+3n,求出ME最大值,则可求出m的最小值;当点N与点D处时,m取得最大值,求解即可.
(1)函数的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),故﹣3a=﹣3,解得:a=1,故函数的表达式为:y=x2﹣2x﹣3;
(2)①过点C作x轴的平行线交抛物线于点C'(2,﹣3),连接AC'交DE于点N,则此时△CAN的周长最小.

设过点A、C'的一次函数表达式为y=kx+b,则:![]() ,解得:
,解得:![]() ,故直线AC'的表达式为:y=﹣x﹣1,当x=1时,y=﹣2,故点N(1,﹣2);
,故直线AC'的表达式为:y=﹣x﹣1,当x=1时,y=﹣2,故点N(1,﹣2);
②如图2,过点C作CG⊥ED于点G.

设NG=n,则NE=3﹣n.
∵∠CNG+∠GCN=90°,∠CNG+∠MNE=90°,∴∠NCG=∠MNE,则tan∠NCG=n=tan∠MNE![]() ,故ME=﹣n2+3n,∴﹣1<0,故ME有最大值,当n
,故ME=﹣n2+3n,∴﹣1<0,故ME有最大值,当n![]() 时,ME
时,ME![]() ,则m的最小值为:
,则m的最小值为:![]() ;
;
如下图所示,当点N与点D重合时,m取得最大值.

过C作CG⊥ED于G.
∵y=x2﹣2x﹣3= y=(x-1)2﹣4,∴D(1,-4),∴CG=OE=1.
∵EG=OC=3∴GD=4-3=1,∴CG=DG=1,∴∠CDG=45°.
∵∠CDM=90°,∴∠EDM=45°,∴△EDM是等腰直角三角形,∴EM=ED=4,∴OM=OE+EM=1+4=5,∴m=5.
故:![]() m≤5.
m≤5.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x![]() +bx+c,经过点A(0,5)和点B(3,2)
+bx+c,经过点A(0,5)和点B(3,2)
(1)求抛物线的解析式:
(2)现有一半径为l,圆心P在抛物线上运动的动圆,问⊙P在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P的坐标:若不存在,请说明理由;
(3)若⊙Q的半径为r,点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人![]() 次测试成绩(单位:分)如下:
次测试成绩(单位:分)如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 乙:
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
回答下列问题:
(1)甲成绩的平均数是 ,乙成绩的平均数是 ;
(2)如果从甲、乙两人![]() 次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于
次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于![]() 分的概率.(用列表或画树状图的方法)
分的概率.(用列表或画树状图的方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线。若∠ABE=∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?( )
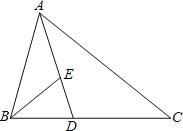
A. 1:6B. 1:9C. 2:13D. 2:15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点.以下四个结论:
①abc>0;
②该抛物线的对称轴在x=﹣1的右侧;
③关于x的方程ax2+bx+c+1=0无实数根;
④![]() ≥2.
≥2.
其中,正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形窗户边框ABCD由矩形AEFD,矩形BNME,矩形CFMN组成,其中AE:BE=1:3.已知制作一个窗户边框的材料的总长是6米,设BC=x(米),窗户边框ABCD的面积为S(米2)
(1)①用x的代数式表示AB;
②求x的取值范围.
(2)求当S达到最大时,AB的长.
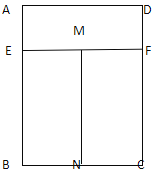
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3),将点O,A,B,C的横坐标、纵坐标都乘以-2.
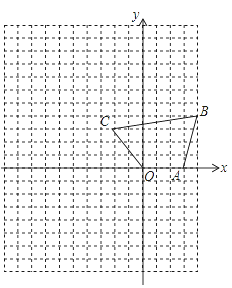
(1)画出以变化后的四个点为顶点的四边形;
(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心及与原图形的相似比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2经过点A(2,1).
(1)求这个函数的解析式;
(2)画出函数的图像,写出抛物线上点A关于y 轴的对称点B 的坐标;
(3)抛物线上是否存在点C,使△ABC的面积等于△OAB面积的一半,若存在,求出C点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.

(1)求该函数的表达式;
(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.
①求线段PQ的最大值;
②若以点P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com