
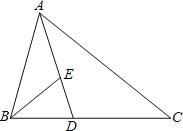
【题目】如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线。若∠ABE=∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?( )
A. 1:6B. 1:9C. 2:13D. 2:15
【答案】D
【解析】
根据已知条件先求得S△ABE:S△BED=2:1,再根据三角形相似求得S△ACD=![]() S△ABE=
S△ABE=![]() S△BED,根据S△ABC=S△ABE+S△ACD+S△BED即可求得答案.
S△BED,根据S△ABC=S△ABE+S△ACD+S△BED即可求得答案.
解:∵AE:ED=2:1,
∴S△ABE:S△BED=2:1,AE:AD=2:3,
∵∠ABE=∠C,∠BAE=∠CAD,
∴△ABE∽△ACD,
∴S△ABE:S△ACD=4:9,
∴S△ACD=![]() S△ABE,
S△ABE,
∵S△ABE=2S△BED,
∴S△ACD=![]() S△ABE=
S△ABE=![]() S△BED,
S△BED,
∵S△ABC=S△ABE+S△ACD+S△BED=2S△BED+![]() S△BED+S△BED=
S△BED+S△BED=![]() S△BED,
S△BED,
∴S△BDE:S△ABC=2:15,
故选:D.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() 和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1)若抛物线C与直线l有交点,求a的取值范围;
(2)当a=-1,二次函数![]() 的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
(3)若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是(____)
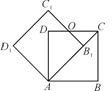
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是( )
A. 抛物线与x轴的一个交点为(4,0)
B. 函数y=ax2+bx+c的最大值为6
C. 抛物线的对称轴是x=![]()
D. 在对称轴右侧,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{﹣1,﹣1}=﹣1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
(1)max{5,2}= ,max{0,3}= ;
(2)若max{3x+1,﹣x+1}=﹣x+1,求x的取值范围;
(3)求函数![]() 与y=﹣x+2的图象的交点坐标,函数
与y=﹣x+2的图象的交点坐标,函数![]() 的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,
的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,![]() }的最小值.
}的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为 3 的正方形![]() 中, 点
中, 点![]() 在射线
在射线![]() 上, 且
上, 且![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,若
,若![]() 沿直线
沿直线![]() 翻折, 点
翻折, 点![]() 落在点
落在点![]() 处 .
处 .
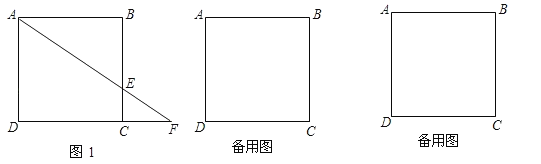
(1)如图1,若点![]() 在线段
在线段![]() 上,求
上,求![]() 的长;
的长;
(2)求![]() 的值;
的值;
(3)如果题设中“![]() ”改为“
”改为“![]() ”, 其它条件都不变, 试写出
”, 其它条件都不变, 试写出![]() 翻折后与正方形
翻折后与正方形![]() 公共部分的面积
公共部分的面积![]() 与
与![]() 的关系式及自变量
的关系式及自变量![]() 的取值范围(只要写出结论,不需写出解题过程) .
的取值范围(只要写出结论,不需写出解题过程) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx﹣3经过点A,B,C,已知点A(﹣1,0),点B(3,0)
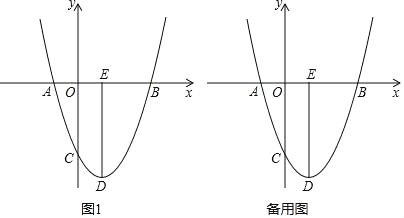
(1)求抛物线的解析式
(2)点D为抛物线的顶点,DE⊥x轴于点E,点N是线段DE上一动点
①当点N在何处时,△CAN的周长最小?
②若点M(m,0)是x轴上一个动点,且∠MNC=90°,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
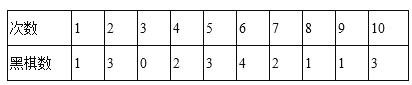
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚B. 50枚C. 40枚D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
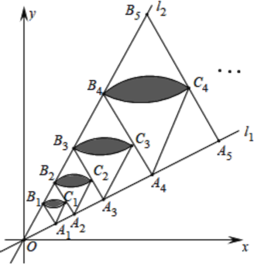
【题目】如图,直线![]() 的解析式是
的解析式是![]() ,直线
,直线![]() 的解析式是
的解析式是![]() ,点
,点![]() 在
在![]() 上,
上,![]() 的横坐标为
的横坐标为![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() ,
,![]() 为邻边在直线
为邻边在直线![]() ,
,![]() 间作菱形
间作菱形![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,以
为圆心,以![]() 为半径画弧得扇形
为半径画弧得扇形![]() 和扇形
和扇形![]() ,记扇形
,记扇形![]() 与扇形
与扇形![]() 重叠部分的面积为
重叠部分的面积为![]() ;延长
;延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() ,
,![]() 为邻边在
为邻边在![]() ,
,![]() 间作菱形
间作菱形![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,以
为圆心,以![]() 为半径画弧得扇形
为半径画弧得扇形![]() 和扇形
和扇形![]() ,记扇形
,记扇形![]() 与扇形
与扇形![]() 重叠部分的面积为
重叠部分的面积为![]() 按照此规律继续作下去,则
按照此规律继续作下去,则![]() __.(用含有正整数
__.(用含有正整数![]() 的式子表示)
的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com