
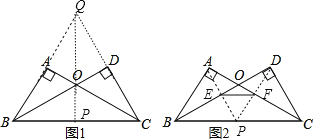
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,限用无刻度直尺完成以下作图:
(1)在图1中作线段BC的中点P;
(2)在图2中,在OB、OC上分别取点E、F,使EF∥BC.

【答案】(1)见解析;(2)见解析.
【解析】
(1)延长BA和CD,它们相交于点Q,然后延长QO交BC于P,则PB=PC,根据线段垂直平分线的逆定理可证明;
(2)连结AP交OB于E,连结DP交OC于F,则EF∥BC.分别证明△BEP≌△CFP,△BEP≌△CFP可得∠APB=∠DPC和∠PEF=∠PFE,根据三角形内角和定理和平角的定义可得∠APB=∠PEF,即可证明EF//BC.
解:(1)如图1,点P为所作,
理由如下:∵∠A=∠D=90°,AC=BD,BC=CB,
∴△ABC≌△DCB
∴∠ABC=∠DCB,∠ACB=∠DBC
∴QB=QC,OB=OC
∴Q,O在BC的垂直平分线上,
∴延长QO交BC于P,就有P为线段BC的中点;
(2)如图2,EF为所作.
理由如下:∵△ABC≌△DCB
∴AB=DC,
又∵∠ABC=∠DCB,BP=PC
∴△ABP≌△DCP
∴∠APB=∠DPC
又∵∠DBC=∠ACB,BP=PC
∴△BEP≌△CFP
∴PE=PF
∴∠PEF=∠PFE,
∵∠APB+∠DPC+∠APD=180°
∠PEF+∠PFE+∠APD=180°
∴∠APB=∠PEF
∴EF//BC.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象经过点A(0,4)和点B(3,0),以线段AB为边在第一象限内作等腰直角△ABC,使∠BAC=90°.

(1)求一次函数的解析式;
(2)求出点C的坐标;
(3)点P是y轴上一动点,当PB+PC最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在![]() 处接到报告:有受灾群众被困于一座遭水淹的楼顶
处接到报告:有受灾群众被困于一座遭水淹的楼顶![]() 处,情况危急!救援队伍在
处,情况危急!救援队伍在![]() 处测得
处测得![]() 在
在![]() 的北偏东
的北偏东![]() 的方向上(如图所示),队伍决定分成两组:第一组马上下水游向
的方向上(如图所示),队伍决定分成两组:第一组马上下水游向![]() 处救人,同时第二组从陆地往正东方向奔跑
处救人,同时第二组从陆地往正东方向奔跑![]() 米到达
米到达![]() 处,再从
处,再从![]() 处下水游向
处下水游向![]() 处救人,已知
处救人,已知![]() 在
在![]() 的北偏东
的北偏东![]() 的方向上,且救援人员在水中游进的速度均为
的方向上,且救援人员在水中游进的速度均为![]() 米/秒.在陆地上奔跑的速度为
米/秒.在陆地上奔跑的速度为![]() 米/秒,试问哪组救援队先到
米/秒,试问哪组救援队先到![]() 处?请说明理由.(参考数据
处?请说明理由.(参考数据![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥BC于点E,过E作EF⊥AC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )

A.9B.8C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,且AD=AC,过点B作BE⊥CD交CD的延长线于点E.
(1)画出符合题意的图形;
(2)求∠BCD的度数;
(3)求证:CD=2BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )

A. y=-2x+24(0<x<12) B. y=-![]() x+12(0<x<24)
x+12(0<x<24)
C. y=2x-24(0<x<12) D. y=![]() x-12(0<x<24)
x-12(0<x<24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com