
| x | … | -3 | -2 | -1 | 0 | 1 | 5 | … |
| y | … | 7 | 0 | -5 | -8 | -9 | 7 | … |
分析 (1)把(-2,0),(-1,-5),(0,-8)代入y=ax2+bx+c中,根据待定系数法即可求得;
(2)把解析式化成顶点式即可求得.
解答 解:(1)把(-2,0),(-1,-5),(0,-8)代入y=ax2+bx+c得
$\left\{\begin{array}{l}{4a-2b+c=0}\\{a-b+c=-5}\\{c=-8}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-8}\end{array}\right.$,
∴二次函数的解析式为y=x2-2x-8;
(2)∵y=x2-2x-8=(x-1)2-9,
∴抛物线顶点坐标为(1,-9),对称轴为直线x=1.
点评 本题考查了待定系数法求二次函数的解析式以及二次函数的顶点坐标和对称轴,熟练掌握待定系数法是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
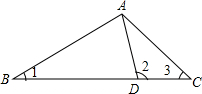 如图,在△ABC中,D是BC上一点,∠1+∠2+∠3=180°,$\frac{CD}{BD}$=$\frac{1}{3}$,则$\frac{AD}{AB}$=( )
如图,在△ABC中,D是BC上一点,∠1+∠2+∠3=180°,$\frac{CD}{BD}$=$\frac{1}{3}$,则$\frac{AD}{AB}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个正方体六个面分别标有字母A、B、C、D、E、F,其展开如图所示,已知:A=x2-2xy、B=A-C,C=3xy+y2,若该正方体相对两个面上的多项式的和相等,试用x、y的代数式表示多项式D,并求当x=-1,y=-2时,多项式D的值.
一个正方体六个面分别标有字母A、B、C、D、E、F,其展开如图所示,已知:A=x2-2xy、B=A-C,C=3xy+y2,若该正方体相对两个面上的多项式的和相等,试用x、y的代数式表示多项式D,并求当x=-1,y=-2时,多项式D的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com