
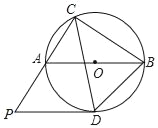
【题目】如图,△ABC内接于⊙O,AB⊙O的直径,∠ACB的平分线交⊙O于D,连接AD和BD,过点D作DP∥AB交CA的延长线于P.
(1)求证:PD是⊙O的切线;
(2)当AC=6,BC=8时,求CD的长.
【答案】(1)详见解析;(2)7![]() .
.
【解析】
(1)欲证明PD是⊙O的切线,只要证明OD⊥PD即可;
(2)如图2中,连接AD、BD,作DE⊥CP与E,DF⊥BC于F.只要证明四边形DECF是正方形且边长为7,即可解决问题;
(1)证明:如图1中,连接OD.
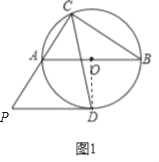
∵∠DCA=∠DCB,
![]()
∴OD⊥AB,
∵AB∥PD,
∴OD⊥PD,
∴PD是⊙O的切线.
(2)如图2中,连接AD、BD,作DE⊥CP与E,DF⊥BC于F.
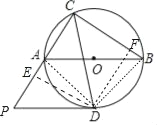
∵AB是直径,
∴∠ECF=∠CED=∠CFD=90°,
∴四边形DECF是矩形,
∵DC平分∠ACB,DE⊥CA,DF⊥CB,
∴DE=DF,
∴四边形DECF是正方形,
∵∵∠DCA=∠DCB,
![]()
∴AD=BD,
![]()
∴ AE=BF,
∴ CE+CF=AC+AE+CB﹣BF=AC+BC=14,
∴ CE=CF=DE=DF=7,
∴CD=![]() CE=7
CE=7![]() .
.


科目:初中数学 来源: 题型:
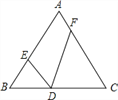
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有5000只鸡准备对外出售。从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出如下的统计图①和图②。请根据相关信息,解答下列问题:
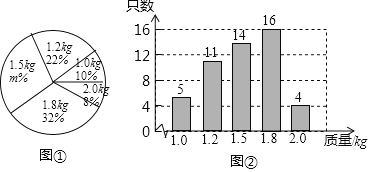
Ⅰ.图①中![]() 的值为 ;
的值为 ;
Ⅱ.求统计的这组数据的平均数、众数和中位数;
Ⅲ.根据样本数据,估计这5000只鸡中,质量为1.0kg的约为多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
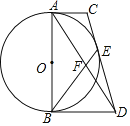
【题目】如图,AB是![]() 的直径,
的直径,![]() ,AC切
,AC切![]() 于点A,点E为
于点A,点E为![]() 上一点,且
上一点,且![]() ,连CE交BD于点D.
,连CE交BD于点D.
![]() 求证:CD为
求证:CD为![]() 的切线;
的切线;
![]() 连AD,BE交于点F,
连AD,BE交于点F,![]() 的半径为2,当点F为AD中点时,求BD.
的半径为2,当点F为AD中点时,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
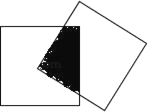
A. 无法确定B. 8cm2C. 16cm2D. 4cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
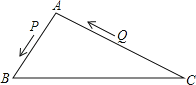
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]()
![]() 过点
过点![]() ,顶点为M点.
,顶点为M点.

(1)求该抛物线的解析式;
(2)试判断抛物线上是否存在一点P,使∠POM=90.若不存在,说明理由;若存在,求出P点的坐标;
(3)试判断抛物线上是否存在一点K,使∠OMK=90,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为< x >,即已知n为正整数,如果n-![]() ≤x<n+
≤x<n+![]() ,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=
,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=![]() 的非负实数x的值为____.
的非负实数x的值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com