练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在四边形ABCD中，已知AB+CD=BC，AB⊥BC，CD⊥BC，请你在BC上作一点E，使△ABE≌△ECD．
    考点：全等三角形的判定
    专题：
    分析：在BC上截取BE=CD，再根据AB+CD=BC，可得AB=EC，再利用SAS定理可判定△ABE≌△ECD．
    解答：解：在BC上截取BE=CD，
    ∵AB+CD=BC，
    ∴AB=EC，
    ∵AB⊥BC，CD⊥BC，
    ∴∠B=∠C=90°，
    在△ABE和△ECD中，
    AB=EC
    ∠B=∠C=90°
    EB=CD
    ，
    ∴△ABE≌△ECD（SAS）．
    点评：此题主要考查了全等三角形的判定，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    点C、D在线段AB上，已知AB=80，AD=65．
    （1）求BD的长；
    （2）若CD=20 求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，DE∥BC，EF∥CG，AD：AB=1：3，AE=3．
    （1）求EC的值；
    （2）求证：AD•AG=AF•AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

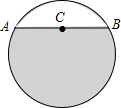    某居民区一处圆形下水管道破裂需要更换，下水管道横截面如图所示，已知污水面宽AB=60m，C为AB中点，且C点距管道底部的距离为90cm，求圆形管道的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上，请在图中画一个格点△A1B1C1使△A1B1C1∽△ABC（相似比不为1），且点都在单位正方形的顶点上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，A，B，C，D是⊙O上的四点，且∠BCD=100°，求∠BOD（弧BCD所对的圆心角）和∠BAD的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列各式中，一定成立的是（　　）
    A、
    		(a+b)2
    =a+b
    B、
    		(a2+1)2
    =a2+1
    C、
    		a2-1
    =
    		a+1
    •
    		a-1
    D、
    a
    b
    =
    1
    b
    		ab

    查看答案和解析>>

    科目：初中数学 来源： 题型：

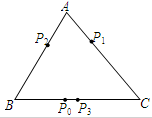    某种“电子爬虫“游戏盘是如图所示的三角形形状，其中AB=6，AC=7，BC=8，爬虫沿游戏盘的边BC、CA、AB按逆时针方向运动．如果爬虫开始时在BC边的P0处，BP0=2．爬虫第一步从P0爬到AC边的P1（第一次落点处），且CP1=CP0；第二步从P1爬到AB边的P2（第二次落点）处，且AP2=AP1；第三步从P2爬到BC边的P3（第三次落点）处，且BP3=BP2；…；爬虫按上述规则一直跳下去，第n次落点Pn（n为正整数），则点P5与P2012之间的距离为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    关于x的方程（m-1）x2-mx+1=0，m
     
    时，它是一元二次方程；m
     
    时，它有两个相等实数根..

    查看答案和解析>>

    同步练习册答案