
【题目】在平面直角坐标系中,有点A(0,4)、B(9,4)、C(12,0)。已知点P从点A出发沿AB路线向点B运动,点Q从点C出发沿CO路线向点O运动,运动速度都是每秒一个单位长度,运动时间为t秒.
(1)当四边形AQCB是平行四边形时,求t值;
(2)连接PQ,当四边形APQO是矩形时,求t值.

【答案】(1)t=9;(2)t=6.
【解析】试题分析:(1)用含![]() 的代数式表示出来CQ,根据平行四边形的性质即可得出
的代数式表示出来CQ,根据平行四边形的性质即可得出![]() 从而得出关于时间
从而得出关于时间![]() 的一元一次方程,解方程即可得出结论;
的一元一次方程,解方程即可得出结论;
(2)用含![]() 的代数式表示出来AP和OQ,根据矩形的性质即可得出
的代数式表示出来AP和OQ,根据矩形的性质即可得出![]() 从而得出关于时间
从而得出关于时间![]() 的一元一次方程,解方程即可得出结论.
的一元一次方程,解方程即可得出结论.
试题解析:(1)当四边形AQCB是平行四边形时,有AB=CQ,
∵A(0,4)、B(9,4),C(12,0),
∴AB=9,OC=12,AB∥OC.
∵CQ=t,
∴t=9.
∴当四边形AQCB是平行四边形时,t的值为9秒.
(2)当四边形APQO是矩形时,有AP=OQ,
∵AP=t,OQ=OCCQ=12t,
∴t=12t,
解得:t=6.
∴当四边形APQO是矩形时,t的值为6秒.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.

(2)类比探究:
如图,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的表达式为
的表达式为![]() ,直线
,直线![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() :
:![]() 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线![]() 、
、![]() 交于点
交于点![]() .
.
(1)求m的值;
(2)求直线![]() 的表达式;
的表达式;
(3)根据图象,直接写出![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x秒,△PBQ的面积为y(cm2). 
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售每个进价为150元和120元的A、B两种型号的足球,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3个 | 4个 | 1200元 |
第二周 | 5个 | 3个 | 1450元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
(1)求A、B两种型号的足球的销售单价;
(2)若商场准备用不多于8400元的金额再购进这两种型号的足球共60个,求A种型号的足球最多能采购多少个?
(3)在![]() 的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.
的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为( )

A.49 B.25 C.13 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
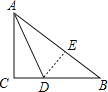
【题目】如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,点D是直线MN上一点,不与点A重合.
(1)若点E是图1中线段AB上一点,且DE=DA,请判断线段DE与DA的位置关系,并说明理由;
(2)请在下面的A,B两题中任选一题解答.
A:如图2,在(1)的条件下,连接BD,过点D作DP⊥DB交线段AC于点P,请判断线段DB与DP的数量关系,并说明理由;
B:如图3,在图1的基础上,改变点D的位置后,连接BD,过点D作DP⊥DB交线段CA的延长线于点P,请判断线段DB与DP的数量关系,并说明理由.

我选择: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com