
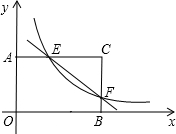
 已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=$\frac{k}{x}$(k>0)的图象与AC边交于点E.
已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=$\frac{k}{x}$(k>0)的图象与AC边交于点E.分析 (1)设出E、F点的坐标,可分别表示出△AOE和△BOF的面积,再根据反比例函数k的几何意义可证明结论;
(2)由条件可分别表示出E、F的坐标,用k可表示出S,再根据函数的性质可求得其最大值,及取得最大值时的k的值.
解答 (1)证明:设E(x1,y1),F(x2,y2),△AOE与△FOB的面积分别为S1,S2,
由题意得${y_1}=\frac{k}{x_1}$,${y_2}=\frac{k}{x_2}$.
∴${S_1}=\frac{1}{2}{x_1}{y_1}=\frac{1}{2}k$,${S_2}=\frac{1}{2}{x_2}{y_2}=\frac{1}{2}k$.
∴S1=S2,即△AOE与△FOB的面积相等.
(2)解:∵OB=4,OA=3,且E、F为反比例函数图象上的两点,
∴E,F两点坐标分别为$E({\frac{k}{3},3})$,$F({4,\frac{k}{4}})$,
如图,连接OE、OF,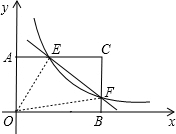
∴${S_{△ECF}}=\frac{1}{2}EC•CF=\frac{1}{2}({4-\frac{1}{3}k})({3-\frac{1}{4}k})$,
∴${S_{△EOF}}={S_{矩形AOBC}}-{S_{△AOE}}-{S_{△BOF}}-{S_{△ECF}}=12-\frac{1}{2}k-\frac{1}{2}k-{S_{△ECF}}=12-k-{S_{△ECF}}$,
∴$S={S_{△OEF}}-{S_{△ECF}}=12-k-2{S_{△ECF}}=12-k-2×\frac{1}{2}({4-\frac{1}{3}k})({3-\frac{1}{4}k})$,
∴$S=-\frac{1}{12}{k^2}+k$.
当$k=-\frac{1}{{2×({-\frac{1}{12}})}}=6$时,S有最大值,Smax=$\frac{-1}{4×(-\frac{1}{12})}$=3.
即当k=6时,S有最大值3.
点评 本题主要考查反比例函数k的意义及二次函数的性质,掌握反比例函数图象上点的坐标满足k=xy是解题的关键.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
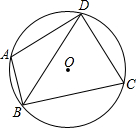 如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:①AD=CD,②$\sqrt{3}$BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,上述结论中正确的个数为( )
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:①AD=CD,②$\sqrt{3}$BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,上述结论中正确的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC与△DEF均为等腰三角形,且△ABC≌△DEF,∠B=∠DEF=90°,点B、C、E、F(C与E重合)在同一条直线上,△ABC从点C出发,沿射线BC方向匀速运动,△DEF的位置保持不动,当点B与点F重合时停止运动.设两个三角形重合部分的面积为y,△ABC平移的距离为x,下面能大致表示y与x间函数关系的图象是( )
如图,△ABC与△DEF均为等腰三角形,且△ABC≌△DEF,∠B=∠DEF=90°,点B、C、E、F(C与E重合)在同一条直线上,△ABC从点C出发,沿射线BC方向匀速运动,△DEF的位置保持不动,当点B与点F重合时停止运动.设两个三角形重合部分的面积为y,△ABC平移的距离为x,下面能大致表示y与x间函数关系的图象是( )| A. |  | B. | 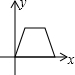 | C. | 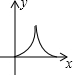 | D. | 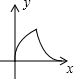 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com