
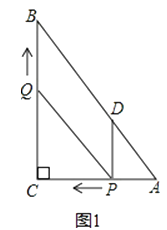
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0���� 
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB= �� PD= ��
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
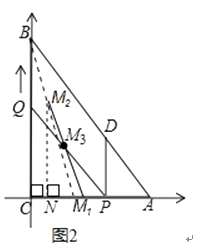
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������
���𰸡�
��1��8��2t��![]() t
t
��2���⣺������
��Rt��ABC�У���C=90�㣬AC=6��BC=8��
��AB=10
��PD��BC��
���APD�ס�ACB��
�� ![]() ����
���� ![]() ��
��
��AD= ![]() t��
t��
��BD=AB��AD=10�� ![]() t��
t��
��BQ��DP��
�൱BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�
��8��2t= ![]() ����ã�t=
����ã�t= ![]() ��
��
��t= ![]() ʱ��PD=
ʱ��PD= ![]() =
= ![]() ��BD=10��
��BD=10�� ![]() ��
�� ![]() =6��
=6��
��DP��BD��
��PDBQ��������
���Q���ٶ�Ϊÿ��v����λ���ȣ�
��BQ=8��vt��PD= ![]() t��BD=10��
t��BD=10�� ![]() t��
t��
Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ��
��PD=BDʱ���� ![]() t=10��
t=10�� ![]() t����ã�t=
t����ã�t= ![]()
��PD=BQ��t= ![]() ʱ����
ʱ���� ![]() =8��
=8�� ![]() ����ã�v=
����ã�v= ![]()
����Q���ٶ�Ϊÿ�� ![]() ����λ����ʱ������
����λ����ʱ������ ![]() �룬�ı���PDBQ������
�룬�ı���PDBQ������
��3���⣺��ͼ2����CΪԭ�㣬��AC���ڵ�ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ��
�����⣬��֪0��t��4����t=0ʱ����M1������Ϊ��3��0������t=4ʱ��M2������Ϊ��1��4����
��ֱ��M1M2�Ľ���ʽΪy=kx+b��
�� ![]() ��
��
��� ![]() ��
��
��ֱ��M1M2�Ľ���ʽΪy=��2x+6��
�ߵ�Q��0��2t����P��6��t��0��
�����˶������У��߶�PQ�е�M3�����꣨ ![]() ��t����
��t����
��x= ![]() ����y=��2x+6��y=��2��
����y=��2x+6��y=��2�� ![]() +6=t��
+6=t��
���M3��ֱ��M1M2�ϣ�
����M2��M2N��x���ڵ�N����M2N=4��M1N=2��
��M1M2=2 ![]()
���߶�PQ�е�M��������·����Ϊ2 ![]() ��λ����
�����
���������⣺��1����������ã�CQ=2t��PA=t�� ��QB=8��2t��
����Rt��ABC�У���C=90�㣬AC=6��BC=8��PD��BC��
���APD=90�㣬
��tanA= ![]() =
= ![]() ��
��
��PD= ![]() t��
t��
�ʴ�Ϊ����1��8��2t�� ![]() t��
t��
��1����������ã�CQ=2t��PA=t����Rt��ABC�У���C=90�㣬AC=6��BC=8��PD��BC�����ɵ�tanA= ![]() =
= ![]() ��������QB��PD��ֵ����2���á�APD�ס�ACB���������AD��BD�ij�����BQ��DP���ɵõ�BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�������ô�ʱDP��BD�ij�����DP��BD�����ж�PDBQ����Ϊ���Σ�Ȼ�����Q���ٶ�Ϊÿ��v����λ���ȣ���Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ���з��̼�����ô𰸣���3����E��AC���е㣬����ME����t=4ʱ����Q���B�غϣ��˶�ֹͣ�����ʱPQ���е�ΪF������EF���ɡ�PMN�ס�PQC���������������εĶ�Ӧ�߳ɱ�����������ô𰸣�
��������QB��PD��ֵ����2���á�APD�ס�ACB���������AD��BD�ij�����BQ��DP���ɵõ�BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�������ô�ʱDP��BD�ij�����DP��BD�����ж�PDBQ����Ϊ���Σ�Ȼ�����Q���ٶ�Ϊÿ��v����λ���ȣ���Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ���з��̼�����ô𰸣���3����E��AC���е㣬����ME����t=4ʱ����Q���B�غϣ��˶�ֹͣ�����ʱPQ���е�ΪF������EF���ɡ�PMN�ס�PQC���������������εĶ�Ӧ�߳ɱ�����������ô𰸣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С���![]() �س������ڶ��������·�ϼ�����·������涨����ʻΪ����������ʻΪ����һ�����ߴ���ʻ��¼���£�����λ��
�س������ڶ��������·�ϼ�����·������涨����ʻΪ����������ʻΪ����һ�����ߴ���ʻ��¼���£�����λ��![]() ��
��
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ���ߴ� |
|
|
|
|
|
|
|
![]() ���չ�ʱ������С����
���չ�ʱ������С����![]() �ص��ĸ�������
�ص��ĸ�������![]() �ض�Զ��
�ض�Զ��
![]() �ڵڼ��μ�¼ʱ��
�ڵڼ��μ�¼ʱ��![]() ����Զ��
����Զ��
![]() ��������ʻÿǧ����
��������ʻÿǧ����![]() �����ʴ�
�����ʴ�![]() �س��������������ٻص�
�س��������������ٻص�![]() �ع����Ͷ�������
�ع����Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1) (2![]() ��3
��3![]() )��
)��![]() �� (2) (
�� (2) (![]() ��
��![]() )2��2
)2��2![]() ��
��![]() ��
��
(3) ![]() �� (4) (
�� (4) (![]() ��2
��2![]() )��
)��![]() ��4
��4![]() ��
��
��5��(![]() ��1)(
��1)(![]() ��1)��(��
��1)��(��![]() )��2��|1��
)��2��|1��![]() |��(��2)0��
|��(��2)0��![]() ��
��
��6��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ������3��2![]() ��(1��
��(1��![]() )2.����˼����С������������̽������a��b
)2.����˼����С������������̽������a��b![]() ��(m��n
��(m��n![]() )2(����a��b��m��n������)������a��b
)2(����a��b��m��n������)������a��b![]() ��m2��2n2��2mn
��m2��2n2��2mn![]() ����a��m2��2n2��b��2mn.����С�����ҵ���һ�ְ�����a��b
����a��m2��2n2��b��2mn.����С�����ҵ���һ�ְ�����a��b![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ������������С���ķ�������������⣺
��ʽ�ӻ�Ϊƽ��ʽ�ķ������������С���ķ�������������⣺
(1)��a��b��m��n��Ϊ������ʱ����a��b![]() ��(m��n
��(m��n![]() )2���ú�m��n��ʽ�ӷֱ��ʾa��b����a��______________��b��________��
)2���ú�m��n��ʽ�ӷֱ��ʾa��b����a��______________��b��________��
(2)������̽���Ľ��ۣ���һ��������a��b��m��n��գ�
________��________![]() ��(________��________
��(________��________![]() )2��
)2��
(3)��a��4![]() ��(m��n
��(m��n![]() )2����a��m��n��Ϊ����������a��ֵ��
)2����a��m��n��Ϊ����������a��ֵ��
(4)�Ի���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��������jiong���ǽ�ʱ�������������һ���������Ƶ����飮��ͼ��ʾ��һ�ű߳�Ϊ20�������ε�ֽƬ����ȥ����һ����Сֱ�������κ�һ�������εõ�һ����������ͼ������Ӱ���֣������ȥ��С�����γ��Ϳ��ֱ�Ϊx��y����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊx��y��
��1���ú���x��y�Ĵ���ʽ��ʾ��ͼ���������������
��2����![]() ʱ�����ʱ�������������
ʱ�����ʱ�������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��֪ʶ��������20���⣬ÿһ���Ե�5�֣������3�֣�
��1��С������68�֣���ôС������˶������⣿
��2��С����ö��Ƚ���70�֡�90�֣�����������С������˼����⣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1�����㣺|��3|+����+1��0�� ![]()
��2������a��1��a��+��a+1��2��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
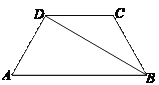
����Ŀ����ͼ���ڵ�������ABCD�У�DC��AB��AD��BC=2��BDƽ����ABC����A��60�㣬��Խ���BD�ij�������ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��3ab2����![]() a2b��2abc��
a2b��2abc��
��2������![]() x2y��3����3xy2����
x2y��3����3xy2����
��3������3xy2��3��![]() x3y����
x3y����
��4����x2+3x����2��4x��x2����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com