
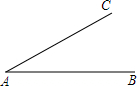
 如图,线段AB和射线AC交于点A,∠A=30°,AB=20.点D在射线AC上,且∠ADB是钝角,写出一个满足条件的AD的长度值:AD=10.
如图,线段AB和射线AC交于点A,∠A=30°,AB=20.点D在射线AC上,且∠ADB是钝角,写出一个满足条件的AD的长度值:AD=10.  亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
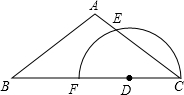 已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求:
已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
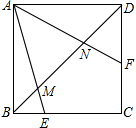 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
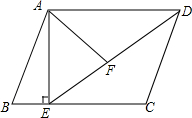 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
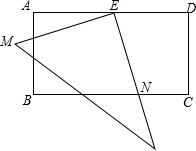 在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
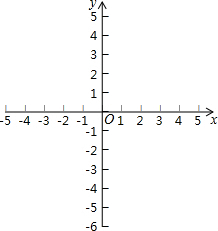 在平面直角坐标系xOy中,等腰三角形ABC的三个顶点A(0,1),点B在x轴的正半轴上,∠ABO=30°,点C在y轴上.
在平面直角坐标系xOy中,等腰三角形ABC的三个顶点A(0,1),点B在x轴的正半轴上,∠ABO=30°,点C在y轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
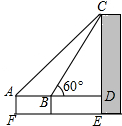 如图,为了测量某建筑物CE的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是45°,然后在水平地面上向建筑物前进了20m,此时自B处测得建筑物顶部的仰角是60°,已知测角仪的高度是1m,请你计算出该建筑物的高度(取$\sqrt{3}$≈1.732,结果精确到1m).
如图,为了测量某建筑物CE的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是45°,然后在水平地面上向建筑物前进了20m,此时自B处测得建筑物顶部的仰角是60°,已知测角仪的高度是1m,请你计算出该建筑物的高度(取$\sqrt{3}$≈1.732,结果精确到1m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com