
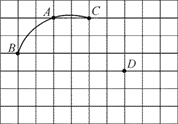
【题目】如图所示,一圆弧过方格的格点A,B,C,在方格中建立平面直角坐标系,使点A的坐标为(-2,4).
(1) 用直尺画出该圆弧所在圆的圆心M的位置,并写出点M的坐标;
(2)判断点D与⊙M的位置关系,并说明理由.
【答案】(1) (-1,1);(2) 见解析.
【解析】
(1)由点A的坐标为(-2,4)可知,x轴在点A的下方4个单位处,y轴在点A的右边2个单位长度处,由此建立其坐标系,然后连接AB、AC,分别画出线段AB和AC的垂直平分线,两条垂直平分线的交点就是所求的点M,然后写出点M的坐标即可;
(2)根据(1)中所得点M的坐标和已知的点A的坐标计算出圆M的半径MA的长,结合点D的坐标和点M的坐标求出MD的长,比较MA和MD的大小即可得出点D与圆M的位置关系.
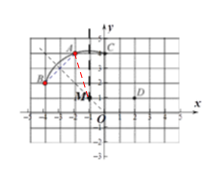
(1)建立的平面直角坐标系和圆心M的位置如下图所示,

由图可得:圆心M的坐标为(-1,1) ;
(2) 如下图,连接MA,
∵A的坐标为(-2,4),点M的坐标为(-1,1),
∴⊙M的半径MB=![]() ,
,
∵点D的坐标为:(2,1),
∴MD=3,
∵3<![]() ,
,
∴点D在⊙M内.


科目:初中数学 来源: 题型:
【题目】仔细想一想,完成下面的说理过程.
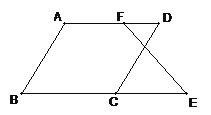
如图,已知AB∥CD,∠B=∠D
求证:∠E=∠DFE.
证明:∵AB∥CD (已知 ),
∴∠B+∠ =180°( )
又∵∠B=∠D(已知 )
∴∠D +∠BCD=180°( )
∴ ( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
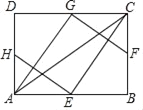
【题目】如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC,GA,GF.已知AG⊥GF,AC=![]() ,则AB的长为__________.
,则AB的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2018次变换后,等边△ABC的顶点C的坐标为_____.
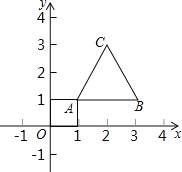
查看答案和解析>>
科目:初中数学 来源: 题型:
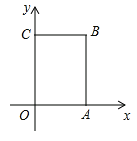
【题目】如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒
从原点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 的路线移动(即沿着长方形的边移动一周).
的路线移动(即沿着长方形的边移动一周).
(1)分别求出![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)当点![]() 移动了
移动了![]() 秒时,求出点
秒时,求出点![]() 的坐标;
的坐标;
(3)在移动过程中,当三角形![]() 的面积是
的面积是![]() 时,求满足条件的点
时,求满足条件的点![]() 的坐标及相应的点
的坐标及相应的点![]() 移动的时间.
移动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com