
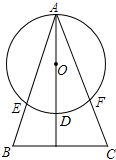
 AD是⊙O的直径,AD⊥BC,AB、AC分别与圆相交于E,F,求证:AB•AE=AF•AC.
AD是⊙O的直径,AD⊥BC,AB、AC分别与圆相交于E,F,求证:AB•AE=AF•AC. 分析 连接DE、DF,如图,先根据圆周角定理由AD是⊙O的直径得到∠AED=∠AFD=90°,而∠AD′B=∠AD′C=90°,则可判断B、D′、D、E四点共圆,C、D′、D、F四点共圆,然后根据切割线定理得AE•AB=AD•AD′,AF•AC=AD•AD′,则AE•AB=AF•AC.
解答 解: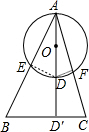 连接DE、DF,设AD⊥BC垂足为D′,
连接DE、DF,设AD⊥BC垂足为D′,
∴AD′⊥BC,如图,
∵AD是⊙O的直径,
∴∠AED=∠AFD=90°,
∵AD′⊥BC,
∴∠AD′B=∠AD′C=90°,
∴B、D′、D、E四点共圆,C、D′、D、F四点共圆,
∴AE•AB=AD•AD′,AF•AC=AD•AD′,
∴AB•AE=AF•AC.
点评 本题考查了相似三角形的判定和性质,圆周角定理,切割线定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
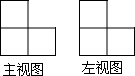 由一些大小相同的小正方体组成的简单几何体的主视图和左视图如图所示.
由一些大小相同的小正方体组成的简单几何体的主视图和左视图如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
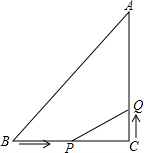 如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com