
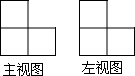
 由一些大小相同的小正方体组成的简单几何体的主视图和左视图如图所示.
由一些大小相同的小正方体组成的简单几何体的主视图和左视图如图所示.分析 (1)由左视图可得第一层立方体的可能个数,由主视图可以看出每一层小正方体的层数和个数,画出三种不同的俯视图即可.
(2)易得这个几何体共有2层,由左视图可得第一层立方体的个数,由主视图可得第二层立方体的可能的个数,相加即可.
解答 解:(1)三种不同的俯视图如图所示: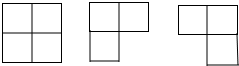
(2)由题中所给出的主视图知物体共二列,且左侧一列高两层,右侧一列最高一层;
由左视图可知左侧两行,右侧一行;
于是,可确定后面一行有3个小正方体,而前面一行可能有1个或2个小正方体.
所以图中的小正方体最少4块,最多5块,
∴n=4或n=5.
点评 本题主要考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查..


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
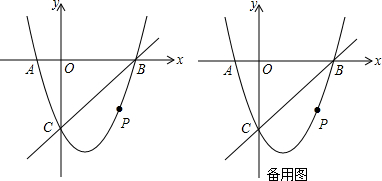
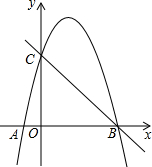 如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
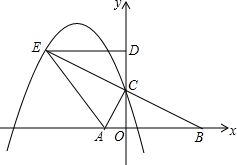 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com