
【题目】数学课上,王老师画好图后并出示如下内容:“己知:![]() 为
为![]() 的直径,
的直径,![]() 过
过![]() 的中点
的中点![]() ,
,![]() 为
为![]() 的切线.”
的切线.”
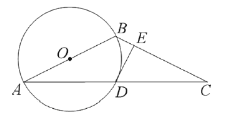
(1)王老师要求同学们根据己知条件,在不添加线段与标注字母的前提下,写出三个正确的结论,并选择其中一个加以证明.
(2)王老师说:如果添加条件“![]() ,
,![]() ”,则能求出
”,则能求出![]() 的直径.请你写出求解过程,
的直径.请你写出求解过程,
【答案】(1)正确的结论可以是:①AB=CB,②∠A=∠C,③DE⊥BC;证明见解析;(2)![]() .
.
【解析】
(1)三个正确的结论:AB=CB,∠A=∠C,DE⊥BC;连接BD、OD,由圆周角定理得∠ADB=90°,则BD⊥AC,由线段垂直平分线的性质得AB=CB,由等腰三角形的性质得∠A=∠C;证OD为△ABC的中位线,则OD∥BC,由切线的性质得出DE⊥OD,得出DE⊥BC;
(2) 由三角函数定义求出CE=2DE=2,由勾股定理得出CD=![]() ,则AD=CD=
,则AD=CD=![]() ,由三角函数定义得
,由三角函数定义得![]() ,则BD=
,则BD=![]() AD=
AD=![]() ,由勾股定理求出AB即可.
,由勾股定理求出AB即可.
解:(1)三个正确的结论:AB=CB,∠A=∠C,DE⊥BC;选择结论“![]() ”进行证明.
”进行证明.
连接BD、OD,如图:
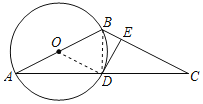
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∵D为AC的中点,
∴AB=CB,
∴∠A=∠C;
∵D为AC的中点,O为AB的中点,
∴OD为△ABC的中位线,
∴OD//BC,
∵DE为⊙O的切线,
∴DE⊥OD,
∴DE⊥BC;
(2)由(1)知,在![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() ,
,
由勾股定理得:![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() 的直径为
的直径为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
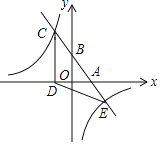
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
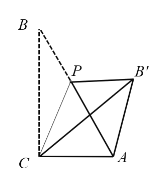
【题目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,点P是AB上一点,连接CP,将∠B沿CP折叠,使点B落在B'处.以下结论正确的有________
①当AB'⊥AC时,AB'的长为![]() ;
;
②当点P位于AB中点时,四边形ACPB'为菱形;
③当∠B'PA=30°时,![]() ;
;
④当CP⊥AB时,AP:AB':BP=1:2:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
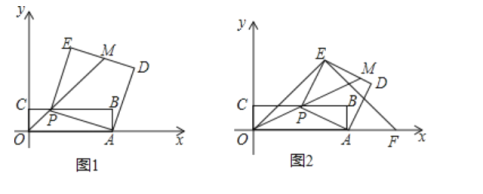
【题目】已知:如图1,矩形OABC的两个顶点A,C分别在x轴,y轴上,点B的坐标是(8,2),点P是边BC上的一个动点,连接AP,以AP为一边朝点B方向作正方形PADE,连接OP并延长与DE交于点M,设![]() .
.
(1)请用含a的代数式表示点P,E的坐标.
(2)如图2,连接OE,并把OE绕点E逆时针方向旋转90°得EF.若点F恰好落在x轴的正半轴上,求a与![]() 的值.
的值.
(3)如图1,若点M为DE的中点,并且![]() ,点
,点![]() 在OP的延长线上,求
在OP的延长线上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 为常数)经过点A
为常数)经过点A![]() 和B
和B![]() .
.
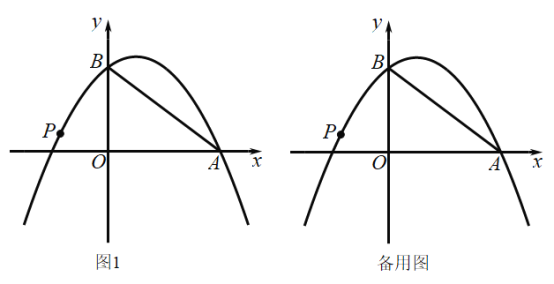
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 是该抛物线上的一动点,设点
是该抛物线上的一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 是以
是以![]() 为直角边的直角三角形时,求
为直角边的直角三角形时,求![]() 的值;
的值;
②若![]() 满足
满足![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州三中初中数学组深知人生最具好奇心和幻想力、创造力的时期是中学时代,经研究,为我校每一个初中生推荐一本中学生素质数育必读书《数学的奥秘》,这本书就是专门为好奇的中学生准备的.这本书不但给于我们知识,解答生活中的疑惑,更重要的是培养我们细致观察、认真思考、勤于动手的能力.经过一学期的阅读和学习,为了了解学生阅读效果,我们从初一、初二的学生中随机各选20名,对《数学的奥秘》此书阅读效果做测试(此次测试满分:100分).通过测试,我们收集到20名学生得分的数据如下:
初一 | 96 | 100 | 89 | 95 | 62 | 75 | 93 | 86 | 86 | 93 |
95 | 95 | 88 | 94 | 95 | 68 | 92 | 80 | 78 | 90 | |
初二 | 100 | 98 | 96 | 95 | 94 | 92 | 92 | 92 | 92 | 92 |
86 | 84 | 83 | 82 | 78 | 78 | 74 | 64 | 60 | 92 |
通过整理,两组数据的平均数、中位数、众数和方差如表:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 87.5 | 91 | m | 96.15 |
初二 | 86.2 | n | 92 | 113.06 |
某同学将初一学生得分按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
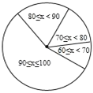
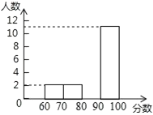
请完成下列问题:
(1)初一学生得分的众数![]() ________;初二学生得分的中位数
________;初二学生得分的中位数![]() ________;
________;
(2)补全频数分布直方图;扇形统计图中,![]() 所对用的圆心角为________度;
所对用的圆心角为________度;
(3)经过分析________学生得分相对稳定(填“初一”或“初二”);
(4)你认为哪个年级阅读效果更好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com