练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在数轴上标出下列各数，并用“＜”把各数连接起来：
    -4，2，-（+
    1
    2
    ），1
    1
    2
    ，-|-1
    1
    2
    |．
    考点：有理数大小比较,数轴
    专题：
    分析：首先在数轴上表示出各个数字，然后比较大小．
    解答：解：在数轴上表示为：
    ，
    用“＜”把各数连接起来为：-4＜-|-1
    1
    2
    |＜-（+
    1
    2
    ）＜1
    1
    2
    ＜2．
    点评：本题考查了有理数的大小比较，解答本题的关键是在数轴上表示出各个数字，然后比较大小．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

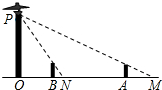    路灯P点距地面9米，身高1.8米的马晓明从距路灯的底部O点20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    △ABC的三边长比为3：5：6，与其相似的△A′B′C′的最长边为15厘米，且△ABC与△A′B′C′的相似比为
    2
    3
    ，则△ABC的最短边长为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某种风扇因季节原因准备打折出售，如果按定价的7.5折出售，将赔30元，如果按定价的9折出售，将赚25元，问这种风扇的定价为多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某种产片的原料提价，因而厂家决定对于产品进行提价，现有三种方案：
    （1）第一次提价p%，第二次提价q%；
    （2）第一次提价q%，第二次提价p%；
    （3）第一、二次提价均为
    p+q
    2
    %．
    其中p，q是不相等的正数，三种方案哪种提价最多？
    （提示：因为p≠q，（p-q）2=p2-2pq+q2＞0，所以p2+q2＞2pq）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC和△ADE中，AC=AB，AE=AD，∠CAB=∠EAD=90°．
    （1）若CE=4，求BD的长；
    （2）求证：CE⊥BD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知直线l：y=kx+b经过点A（0，8）且平行于直线y=-2x 
    （1）求直线1的解析式；
    （2）如果直线l经过P（m，2），求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小张与小亮站在全长为400米的环形跑道上，两个人之间的距离是50米，两人同时起跑，已知小张的速度为每秒8米，小亮的速度为每秒7米，两人沿逆时针方向跑，经多少时间小张第一次追上小亮？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

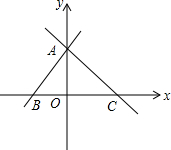    因为一次函数y=kx+b与y=-kx+b（k≠0）的图象关于y轴对称，所以我们定义：函数y=kx+b与y=-kx+b（k≠0）互为“镜子”函数．
    （1）请直接写出函数y=3x-2的“镜子”函数：
     
    ；
    （2）如果一对“镜子”函数y=kx+b与y=-kx+b（k≠0）的图象交于点A，且与x轴交于B、C两点，如图所示，若△ABC是等腰直角三角形，∠BAC=Rt∠，且它的面积是16，求这对“镜子”函数的解析式．

    查看答案和解析>>

    同步练习册答案