
����Ŀ��ij�����Ǿ���A�ͺŲʵ磬�������·�ÿ̨�ʵ��ۼ���ȥ��ͬ����Ƚ���500Ԫ����������ʵ��������ͬ����ȥ�����۶�Ϊ5��Ԫ���������۶�Ϊ4��Ԫ��
��1����ȥ�����·�ÿ̨A�ͺŲʵ��ۼ��Ƕ���Ԫ��
��2��Ϊ�˸��ƾ�Ӫ�������Ǿ����پ���B�ͺŲʵ磮��֪A�ͺŲʵ�ÿ̨������Ϊ1800Ԫ��B�ͺŲʵ�ÿ̨������Ϊ1500Ԫ��������Ԥ���ò�����3.3��Ԫ�Ҳ�����3.2��Ԫ���ʽ������ֲʵ繲20̨�������ļ��ֽ���������
��3������������A�ͺŲʵ������ԭ�۳��ۣ�B�ͺŲʵ���ÿ̨1800Ԫ�ļ۸���ۣ��������ʵ�ȫ��������ǰ���£���ν�������ʹ�����ǻ��������������Ƕ��٣�
���𰸡���1��ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���2500Ԫ����2����4�ֽ�������������һ������A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨��������������A���ͺŵIJʵ�8̨��B���ͺŲʵ�12̨��������������A���ͺŵIJʵ�9̨��B���ͺŲʵ�11̨�������ģ�����A���ͺŵIJʵ�10̨��B���ͺŲʵ�10̨����3���������ʵ�ȫ��������ǰ���£�����A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨����ʹ�����ǻ���������������5300Ԫ��
��������
��1��������ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���xԪ���ٸ���ȥ�����������������ͬ�г����̣����ɵý⣻
��2������������ǹ���A���ͺŵIJʵ�ą���ٸ��������г�һԪһ�β���ʽ�飬��ü��ɣ�
��3��������������ΪwԪ���ٸ��������г�һ�κ����������ж���a��7ʱ��wȡ�����ֵ����ʱw��5300�����ɵý�.
�⣺��1����ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���xԪ��
![]() ��
��
��ã�x��2500��
�����飬x��2500��ԭ��ʽ���̵Ľ⣬
��ȥ�����·�ÿ̨A�ͺŲʵ��ۼ���2500Ԫ��
��2��������ǹ���A���ͺŵIJʵ�ą��
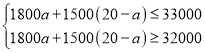 ��
��
��ã�![]() ��a��10��
��a��10��
��a������
��a��7��8��9��10��
������4�ֽ���������
����һ������A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨��
������������A���ͺŵIJʵ�8̨��B���ͺŲʵ�12̨��
������������A���ͺŵIJʵ�9̨��B���ͺŲʵ�11̨��
�����ģ�����A���ͺŵIJʵ�10̨��B���ͺŲʵ�10̨��
��3����������ΪwԪ��
w����2500��500��1800��a+��1800��1500����20��a������100a+6000��
��a��7��8��9��10��
�൱a��7ʱ��wȡ�����ֵ����ʱw��5300��
���������ʵ�ȫ��������ǰ���£�����A���ͺŵIJʵ�7̨��B���ͺŲʵ�13̨����ʹ�����ǻ���������������5300Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
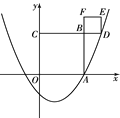
����Ŀ����ͼ��������![]() ��
��![]() �������ύ�ڵ�A��3��0������OAΪ����
�������ύ�ڵ�A��3��0������OAΪ����![]() ���Ϸ���������OABC���ӳ�CB���������ڵ�D������BDΪ��������������BDEF����
���Ϸ���������OABC���ӳ�CB���������ڵ�D������BDΪ��������������BDEF����![]() = ����E�������� ��
= ����E�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
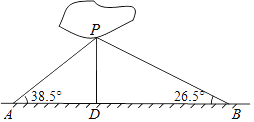
����Ŀ����ͼ��������������Ϻ�����һС����������һ����ֱ�Ĺ۹�С�����־�����С����һ����۹�С����ֱ��С��PD��С����С���ϲ���������ݣ�AB=200.0�ף���PAB=38.5������PBA=26.5���������С�����С��PD�ij����������ȷ��0.1�ף� ���ο����ݣ�sin38.5���0.62��cos38.5���0.78��tan38.5���0.80��sin26.5���0.45��cos26.5���0.89��tan26.5���0.50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
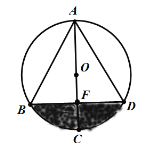
����Ŀ����ͼ����֪�ڡ�O�У�AB=4![]() �� AF=6��AC��ֱ����AC��BD��F��ͼ����Ӱ���ֵ�����ǣ�������
�� AF=6��AC��ֱ����AC��BD��F��ͼ����Ӱ���ֵ�����ǣ�������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
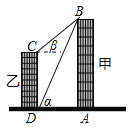
����Ŀ����ͼ���߶�AB��CD�ֱ��ʾ������������ĸߣ�BA��AD��CD��DA������ֱ�ΪA��D����D��B���������Ϊ60������C����B���������Ϊ30����������ĸ�AB=30��
��1����ס�����������֮��ľ���AD��
��2�����ҽ�����ĸ�CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
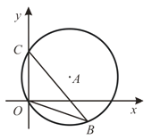
����Ŀ����ͼ��ֱ��Ϊ10�ġ�A������C(0,5)�͵�O (0,0)��B��y���Ҳ��A�Ż���һ��,���OBC ������ֵΪ _________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+c�ĶԳ���Ϊֱ��x����1��ͼ�����1��0���㣬����ͼ����ͼ��ʾ�������ж��У���abc��0����b2��4ac��0����9a��3b+c��0�������㣨��0.5��y1��������2��y2�������������ϣ���y1��y2����5a��2b+c��0��������ȷ�ĸ����У�������
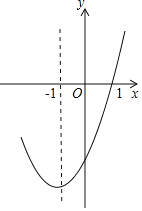
A. 2B. 3C. 4D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȡ�ת���������һ���˼�뷽��������ѧѧϰ���о��о����õ���������һ���������벹��������
ԭ�⣺��ͼ1����ABCD�У���E��BC���ϵ��е㣬��F���߶�AE��һ�㣬BF���ӳ��߽�����CD�ڵ�G����![]() =3����
=3����![]() ��ֵ��
��ֵ��
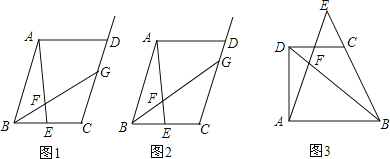
��1������̽��
��ͼ1�У�����E��EH��AB��BG�ڵ�H����AB��EH��������ϵ�� ��CG��EH��������ϵ�� ��![]() ��ֵ��
��ֵ��
��2���������
��ͼ2����ԭ��������£���![]() =m��m��0������
=m��m��0������![]() ��ֵ�� ���ú�m�Ĵ���ʽ��ʾ������д�������̣�
��ֵ�� ���ú�m�Ĵ���ʽ��ʾ������д�������̣�
��3����չǨ��
��ͼ3������ABCD�У�DC��AB����E��BC�ӳ�����һ�㣬AE��BD�ཻ�ڵ�F����![]() =a��
=a��![]() =b��a��0��b��0������
=b��a��0��b��0������![]() ��ֵ�� ���ú�a��b�Ĵ���ʽ��ʾ����
��ֵ�� ���ú�a��b�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ҹ۹��δ��Ӹۿ�A�Ա�ƫ��60��ķ�����۹۹⣬����80������C��ʱ�����˲෭�����¹ʣ���������������źţ�һ���ڸۿ���������ĺ������ӵ�����źţ�����¹ʴ������ı�ƫ��37�㷽��������ÿСʱ40������ٶ�ǰ����Ԯ�����������¹ʴ�C�������ʱ���ԼΪ����λ��Сʱ����������
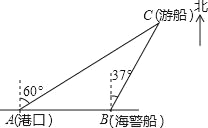
A. ![]() B.
B. ![]() C. sin37��D. cos37��
C. sin37��D. cos37��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com