
【题目】已知直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,
点, ![]() 为
为![]() 的中点,
的中点, ![]() 为射线
为射线![]() 上一点,连
上一点,连![]() ,将
,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得线段
得线段![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
【解析】根据题意,画出图形(如图所示),直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,
点, ![]() 为
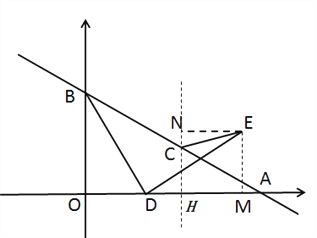
为![]() 的 中点,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.过点E作EM⊥x轴于点M,过点E作NC⊥x轴,过点E作EN⊥NC于点N,因为BD⊥DE,∠BOD=∠AMD=90°,即可证得∠ODB=∠MED,再由BD=DE,根据AAS即可判定△ODB≌△MED,根据全等三角形的对应边相等可得OD=EM,OB=DM=2,设OD=EM=m,则OM=2+m,由点C为AB的中点可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根据勾股定理可得
的 中点,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.过点E作EM⊥x轴于点M,过点E作NC⊥x轴,过点E作EN⊥NC于点N,因为BD⊥DE,∠BOD=∠AMD=90°,即可证得∠ODB=∠MED,再由BD=DE,根据AAS即可判定△ODB≌△MED,根据全等三角形的对应边相等可得OD=EM,OB=DM=2,设OD=EM=m,则OM=2+m,由点C为AB的中点可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根据勾股定理可得![]() ,当
,当![]() 时,
时, ![]() 最小,最小为
最小,最小为![]() ,所以EC最小为
,所以EC最小为![]() .
.


科目:初中数学 来源: 题型:
【题目】观察下列等式的规律,解答下列问题:
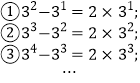
(1)按此规律,第④个等式为_________;第![]() 个等式为_______;(用含
个等式为_______;(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
(2)按此规律,计算:
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
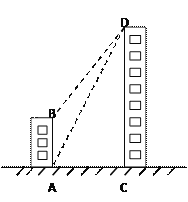
【题目】如图,一栋居民楼AB的高为16米,远处有一栋商务楼CD,小明在居民楼的楼底A处测得商务楼顶D处的仰角为![]() ,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为
,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为![]() .其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
.其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
(参考数据: ![]() ,
, ![]() .结果精确到0.1米)
.结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场对外批发某品脾的玩具,其价格与件数关系如图所示,请你根据图中描述判断:下列说法中错误的是( )

A. 当件数不超过30件时,每件价格为60元
B. 当件数在30到60之间时,每件价格随件数增加而减少
C. 当件数为50件时,每件价格为55元
D. 当件数不少于60件时,每件价格都是45元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (1,0)和点
(1,0)和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() =1.
=1.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)连接![]() 、
、![]() ,若△
,若△![]() 的面积为6,求此抛物线的解析式;
的面积为6,求此抛物线的解析式;
(3)在(2)的条件下,点![]() 为
为![]() 轴正半轴上的一点,点
轴正半轴上的一点,点![]() 与点
与点![]() ,点
,点![]() 与点
与点![]() 关于点
关于点![]() 成中心对称,当△
成中心对称,当△![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
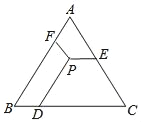
【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
A. 18B. 9![]()
C. 6D. 条件不够,不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com