
【题目】如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系,请从你所得两个关系中选出任意一个,说明你探究的结论的正确性. 
结论:
(1)
(2) 选择结论: , 说明理由.
【答案】
(1)∠APC+∠PAB+∠PCD=360°
(2)∠APC=∠PAB+∠PCD;∠APC+∠PAB+∠PCD=360°或∠APC=∠PAB+∠PCD
【解析】解:(1)∠APC+∠PAB+∠PCD=360°. 理由如下:过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
2)∠APC=∠PAB+∠PCD.
理由如下:过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,
∴∠APC=∠PAB+∠PCD.
故答案为:∠APC+∠PAB+∠PCD=360°,∠APC=∠PAB+∠PCD;∠APC+∠PAB+∠PCD=360°或∠APC=∠PAB+∠PCD.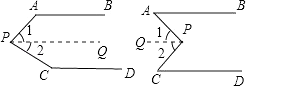
(1)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,同旁内角互补,即可求得∠PAB+∠1=180°,∠2+∠PCD=180°,则可得∠APC+∠PAB+∠PCD=∠PBA+∠1+∠2+∠PCD=360°;(2)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠PAB,∠2=∠PCD,则可得∠APC=∠PAB+∠PCD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的为( )
A.打开电视机,正在播放广告B.任意画一个三角形,它的内角和等于180°
C.掷一枚硬币,正面朝上D.在只有红球的盒子里摸到白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点A、B、C均在格点上.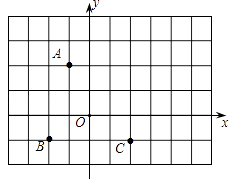
(1)请直接写出点A、B、C的坐标;
(2)若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B、C、D、A,并求出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“PM2.5”指数是空气中可入肺颗粒物的含量,是空气质量的指标之一.下表为A市1﹣12月“PM2.5月平均指数”(单位:微克/立方米)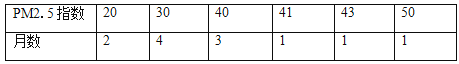
(1)求这12个月“PM2.5月平均指数”的众数、中位数、平均数;
(2)根据《环境空气质量标准》,宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”,请你判断A市是否为宜居城市?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=(x﹣3)2﹣4向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )
A.y=(x﹣4)2﹣6B.y=(x﹣2)2﹣2
C.y=(x﹣1)2﹣3D.y=(x﹣4)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解全校的耗电情况,抽查了10天中全校每天的耗电量,数据如下表:(单位:kW·h)
(1)写出上表中数据的众数和平均数;
(2)由上题获得的数据,估计该校某月的耗电量(按30天计);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com