
 如图,在平面直角坐标系xOy中,?OABC的顶点A,B的坐标分别为(6,0),(7,3),将?OABC绕点O逆时针方向旋转得到?OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为
如图,在平面直角坐标系xOy中,?OABC的顶点A,B的坐标分别为(6,0),(7,3),将?OABC绕点O逆时针方向旋转得到?OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为| 6 | ||
|
| 3 |
| 4 |
| EF |
| OF |
| 3 |
| 4 |
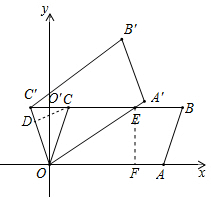 解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),
解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6 | ||
|
| OD |
| OC |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| EF |
| OF |
| EF |
| tan∠AOE |


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
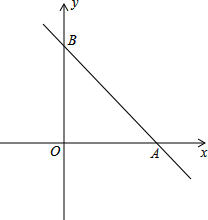 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 水果品牌 | A | B | C |
| 每辆汽车载重量(吨) | 6 | 5 | 4 |
| 每吨水果可获利润(万元) | 0.5 | 0.6 | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).查看答案和解析>>
科目:初中数学 来源: 题型:
 某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表:
某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表:| 项目 | 人数 | 百分比 |
| 没有剩 | 80 | 40% |
| 剩少量 | a | 20% |
| 剩一半 | 50 | b |
| 剩大量 | 30 | 15% |
| 合计 | 200 | 100% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com