
【题目】(1)如图1,网格中每个小正方形的边长为1,点A,B均在格点上.则线段AB的长为 .请借助网格,仅用无刻度的直尺在AB上作出点P,使AP=![]() .
.
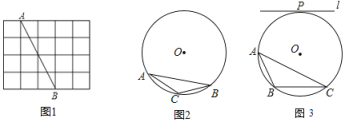
(2)⊙O为△ABC的外接圆,请仅用无刻度的直尺,依下列条件分别在图2,图3的圆中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法,请下结论注明你所画的弦).
①如图2,AC=BC;
②如图3,P为圆上一点,直线l⊥OP且l∥BC.
【答案】(1)2![]() ,画图作出点P见解析;(2)①画图见解析,② 画图见解析.
,画图作出点P见解析;(2)①画图见解析,② 画图见解析.
【解析】
(1)利用勾股定理列式求出AB=2![]() ,然后利用相似三角形的判定与性质构造相似三角形,满足AP:BP=2:1即可;
,然后利用相似三角形的判定与性质构造相似三角形,满足AP:BP=2:1即可;
(2)①过点C作直径CD,由于AC=BC,弧AC=弧BC,根据垂径定理的推理得CD垂直平分AB,所以CD将△ABC分成面积相等的两部分;
②连结PO并延长交BC于E,过点A、E作弦AD,由于直线l与⊙O相切于点P,根据切线的性质得OP⊥l,而l∥BC,则PE⊥BC,根据垂径定理得BE=CE,所以弦AE将△ABC分成面积相等的两部分.
(1)AB=![]() 2
2![]() ,作图如图所示;所以,AP=
,作图如图所示;所以,AP=![]() 时AP:BP=2:1.
时AP:BP=2:1.
点P如图所示.取格点M,N,连接MN交AB于P,则点P即为所求;
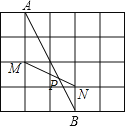
(2)①如图1,CD即为所求;
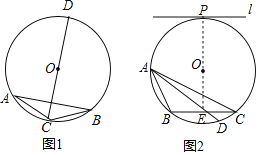
②如图2,CD即为所求.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
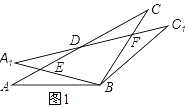
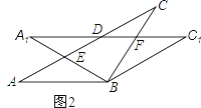
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知直线![]() 分别于
分别于![]() 轴和
轴和![]() 轴交于
轴交于![]() ,
,![]() 两点,将抛物线
两点,将抛物线![]() 平移,得到抛物线
平移,得到抛物线![]() ,使抛物线
,使抛物线![]() 过点
过点![]() ,
,![]() 两点.
两点.
①求交点![]() ,
,![]() 的坐标;
的坐标;
②求抛物线![]() 的函数表达式;
的函数表达式;
③求抛物线的顶点坐标和对称轴方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
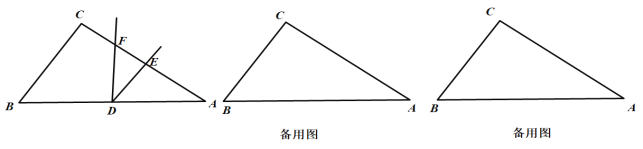
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是斜边
是斜边![]() 的中点,以
的中点,以![]() 为顶点,作
为顶点,作![]() ,
,![]() 的两边交边
的两边交边![]() 于点
于点![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合)
重合)
(1)当![]() 时,求
时,求![]() 的长度;
的长度;
(2)当![]() 绕点
绕点![]() 转动时,设
转动时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围.
的取值范围.
(3)联结![]() ,是否存在点
,是否存在点![]() ,使△
,使△![]() 与△
与△![]() 相似?若存在,请求出此时
相似?若存在,请求出此时![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83 乙:88,79,90,81,72.
(1)求甲、乙两名同学测试成绩的方差;
(2)请你选择一个角度来判断选拔谁参加比赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
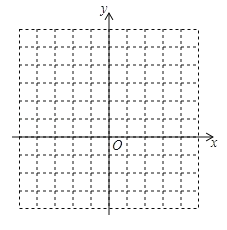
【题目】在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
(1)求这条抛物线的函数表达式;
(2)求该抛物线的顶点坐标;
(3)在给定坐标系内画出这条抛物线.
查看答案和解析>>
科目:初中数学 来源: 题型:
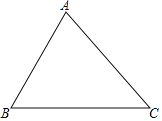
【题目】如图,已知△ABC.(1)请用圆规和直尺作出⊙P,使圆心P到AB边和BC边的距离相等,且⊙P经过A,B两点(保留作图痕迹,不写作法和证明);
(2)若∠B=60°,AB=6,求⊙P的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com