
【题目】2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).

(1)分数段在-----范围的人数最多;
(2)全校共有多少人参加比赛?
(3)学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.
科目:初中数学 来源: 题型:
【题目】某商场准备采购一批特色商品,经调查,用5000元采购![]() 型商品的件数是用2000元采购
型商品的件数是用2000元采购![]() 型商品的件数的2倍,一件
型商品的件数的2倍,一件![]() 型商品的进价比一件
型商品的进价比一件![]() 型商品的进价多10元.
型商品的进价多10元.
(1)求一件![]() ,
,![]() 型商品的进价分别为多少元?
型商品的进价分别为多少元?
(2)若该商场购进![]() ,
,![]() 型商品共200件进行试销,其中
型商品共200件进行试销,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型商品的件数,且不小于80件.已知
型商品的件数,且不小于80件.已知![]() 型商品的售价为80元/件,
型商品的售价为80元/件,![]() 型商品的售价为60元/件,且
型商品的售价为60元/件,且![]() ,
,![]() 型商品均全部售出.设购进
型商品均全部售出.设购进![]() 型商品
型商品![]() 件,求该商场销售完这批商品的利润
件,求该商场销售完这批商品的利润![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,商场决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元
元![]() ,若该商场售完
,若该商场售完![]() 、
、![]() 型所有商品并捐献资金后获得的最大收益是4800元,求出
型所有商品并捐献资金后获得的最大收益是4800元,求出![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 四张不透明的卡片,除正面上的图案不同外,其他均相同,将这四张卡片背 面向上洗匀后放在桌面上.
四张不透明的卡片,除正面上的图案不同外,其他均相同,将这四张卡片背 面向上洗匀后放在桌面上.
(1)从中随机取出一张卡片,卡片上的图案是中心对称图形的概率是_____;
(2)若从四张卡片中随机拿出两张卡片,请用画树状图或列表的方法,求抽取的两张卡片都是轴对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多8元,用1800元购买的科普书的数量与用l000元购买的文学书的数量相同.
(1)求去年购买的文学书和科普书的单价各是多少元;
(2)这所学校今年计划再购买这两种文学书和科普书共200本,且购买文学书和科普书的总费用不超过2088元.今年文学书的单价比去年提高了20%,科普书的单价与去年相同,且每购买1本科普书就免费赠送1本文学书,求这所学校今年至少要购买多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的半径为5,点A的坐标为(3,0),
的半径为5,点A的坐标为(3,0),![]() 与x轴相交于点B,C,交y轴正半轴于点D.
与x轴相交于点B,C,交y轴正半轴于点D.
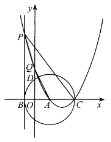
(1)求点B,D的坐标;
(2)过点B作![]() 的切线,与过点A,C的抛物线交于点P.抛物线交y轴正半轴于点Q.若P的纵坐标为t,四边形PQAC的面积为y.
的切线,与过点A,C的抛物线交于点P.抛物线交y轴正半轴于点Q.若P的纵坐标为t,四边形PQAC的面积为y.
①求y与t的函数关系式;
②若△PBO与△DOA相似,求![]() 取最小值时m的值.
取最小值时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购进甲、乙两种规格的书架,经市场调查发现有线上和线下两种购买方式,具体情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
甲 | 240 | 0 | 210 | 20 |
乙 | 300 | 0 | 250 | 30 |
(1)如果在线下购买甲、乙两种书架共30个,花费8280元,求甲、乙两种书架各购买了多少个?
(2)如果在线上购买甲、乙两种书架共30个,且购买乙种书架的数量不少于甲种书架的3倍,请求出花费最少的购买方案及花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 抛物线
抛物线![]() 经过点
经过点![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
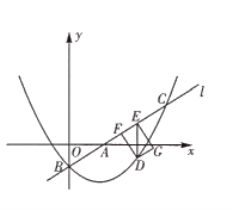
![]() 求
求![]() 的值和抛物线的解析式
的值和抛物线的解析式
![]() 点
点![]() 在抛物线上,
在抛物线上,![]() 轴交直线
轴交直线![]() 于点
于点![]() 点
点![]() 在直线
在直线![]() 上,且四边形
上,且四边形![]() 为矩形.设点
为矩形.设点![]() 的横坐标为
的横坐标为![]() 矩形
矩形![]() 的周长为
的周长为![]() 求
求![]() 与
与![]() 的函数关系式以及
的函数关系式以及![]() 的最大值
的最大值
![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别与
分别与![]() 点对应),若
点对应),若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com