
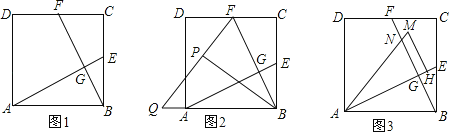
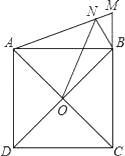
【题目】如图1,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF,交点为G.若正方形的边长为2.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求AQ的长;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,求四边形MNGH的面积.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)运用Rt△ABE≌Rt△BCF,再利用角的关系求得∠BGE=90°即可;
(2)首先利用折叠的性质和平行线的性质得到QF=QB,然后在Rt△QPB中,利用勾股定理即可解决问题.
(3)首先证明△AGN∽△AHM,再根据面积比等于相似比的平方,求得S△AGN=![]() ,再利用S四边形GHMN=S△AHM﹣S△AGN求解.
,再利用S四边形GHMN=S△AHM﹣S△AGN求解.
(1)证明: ∵四边形ABCD是正方形,
![]() .
.
∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE.
在Rt△ABE和Rt△BCF中,
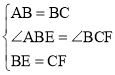 ,
,
∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF.
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF.
(2)由折叠的性质得FP=FC,∠PFB=∠BFC,∠FPB=∠BCF =90°,
∵四边形ABCD是正方形,
![]() .
.
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB.
∵PF=FC=1,PB=BC=2,
在Rt△BPQ中,设QB=x,
∴x2=(x﹣1)2+22,
∴x=![]() ,
,
∴AQ=BQ﹣AB=![]() .
.
(3)解:![]() ,
,
![]() .
.
由旋转的性质可知,![]() .
.
∵∠BAE=∠EAM,AE⊥BF,
∴AN=AB=2.
∵∠AHM=90°,
![]() .
.
![]() .
.
∴GN∥HM,
∴△AGN∽△AHM,
∴![]() =(
=(![]() )2.
)2.
![]() ,
,
∴![]() =(
=( ![]() )2,
)2,
∴S△AGN=![]() ,
,
∴S四边形GHMN=S△AHM﹣S△AGN=1﹣![]() =
=![]() ,
,
∴四边形GHMN的面积是 ![]() .
.


科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )
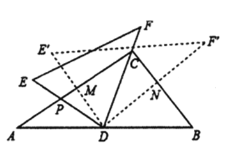
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
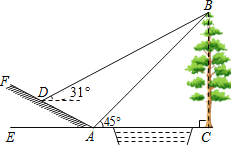
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B两地的运费如下表所示:
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=![]() ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧几里得在《几何原本》中,记载了用图解法解方程![]() 的方法,类似地可以用折纸的方法求方程
的方法,类似地可以用折纸的方法求方程![]() 的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片
的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() ,然后通过折叠使
,然后通过折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() ,类似地,在
,类似地,在![]() 上折出点
上折出点![]() 使
使![]() 。此时,
。此时,![]() 的长度可以用来表示方程
的长度可以用来表示方程![]() 的一个正根;乙:如图2,裁一张边长为1的正方形的纸片
的一个正根;乙:如图2,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() N,然后通过沿线段
N,然后通过沿线段![]() 折叠使
折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() 。此时,
。此时,![]() 的长度可以用来表示方程
的长度可以用来表示方程![]() 的一个正根;甲、乙两人的做法和结果( )。
的一个正根;甲、乙两人的做法和结果( )。

A.甲对,乙错B.乙对,甲错C.甲乙都对D.甲乙都错
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数![]() 的图象绕点
的图象绕点![]() 旋转
旋转![]() ,得到新函数
,得到新函数![]() 的图象,我们称
的图象,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图象的对称轴与
的图象的对称轴与![]() 轴交点坐标为
轴交点坐标为![]() .
.
(1)填空:![]() 的值为 (用含
的值为 (用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的解析式;
的解析式;
(3)当![]() 时,
时,![]() 的图象与
的图象与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧).与
的右侧).与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 原点
原点![]() 逆时针旋转
逆时针旋转![]() ,得到它的对应线段
,得到它的对应线段![]() ,若线
,若线![]() 与
与![]() 的图象有公共点,结合函数图象,求
的图象有公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
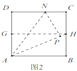
【题目】如图,已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,抛物线
,抛物线![]() 的顶点是
的顶点是![]() ,且与
,且与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 是抛物线上一个动点,过点
是抛物线上一个动点,过点![]() 作
作![]() 于点
于点![]() .
.
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 当点
当点![]() 运动到何处时,线段PG的长取最小值?最小值为多少?
运动到何处时,线段PG的长取最小值?最小值为多少?
![]() 若点
若点![]() 是抛物线对称轴上任意点,点
是抛物线对称轴上任意点,点![]() 是抛物线上一动点,是否存在点
是抛物线上一动点,是否存在点![]() 使得以点
使得以点![]() 为顶点的四边形是菱形?若存在,请你直接写出点
为顶点的四边形是菱形?若存在,请你直接写出点![]() 的坐标;若不存在,请你说明理由.
的坐标;若不存在,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
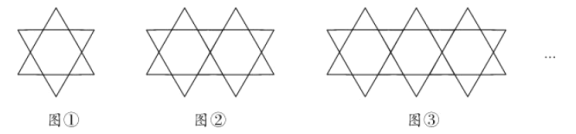
【题目】将大小相同的正三角形按如图所示的规律拼图案,其中第①个图案中有6个小三角形和1个正六边形;第②个图案中有10个小三角形和2个正六边形;第③个图案中有14个小三角形和3个正六边形;…;按此规律排列下去,已知一个正六边形的面积为![]() ,一个小三角形的面积为
,一个小三角形的面积为![]() ,则第③个图案中所有的小三角形和正六边形的面积之和为______.(结果用含
,则第③个图案中所有的小三角形和正六边形的面积之和为______.(结果用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com