
分析 根据抛物线的最值问题得到$\frac{4{m}^{2}-{4}^{2}}{4m}$=3,解得m1=4,m2=-1,然后根据二次函数有最小值确定m的值.
解答 解:根据题意得$\frac{4{m}^{2}-{4}^{2}}{4m}$=3,
解得m1=4,m2=-1,
而二次函数y=mx2+4x+m的最小值,
所以m>0,
所以m=4.
故答案为4.
点评 本题考查了二次函数的最值:当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$.当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
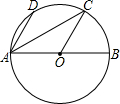 如图,AB是⊙O的直径,点D,C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC等于( )
如图,AB是⊙O的直径,点D,C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC等于( )| A. | 20° | B. | 30° | C. | 25° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com