
【题目】(1)发现:如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,分别以
上的一点,分别以![]() 为边向外作等边三角形
为边向外作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() ,
,![]() ,相交于点
,相交于点![]() .
.

①线段![]() 与
与![]() 的数量关系为:___________;
的数量关系为:___________;![]() 的度数为__________.
的度数为__________.
②![]() 可看作
可看作![]() 经过怎样的变换得到的?____________________________.
经过怎样的变换得到的?____________________________.
(2)应用:如图![]() ,若点
,若点![]() 不在一条直线上,(1)的结论①还成立吗?请说明理由;
不在一条直线上,(1)的结论①还成立吗?请说明理由;
(3)拓展:在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() ,
,![]() 两点之间的距离.
两点之间的距离.
【答案】(1)①![]() ,
,![]() ;(2)依然成立,见解析;(3)
;(2)依然成立,见解析;(3)![]() .
.
【解析】
(1)①证明△ABE≌△CBD,根据全等三角形的性质即可求出线段![]() 与
与![]() 的数量关系;根据三角形外角的性质即可求出
的数量关系;根据三角形外角的性质即可求出![]() 的度数.
的度数.
②根据旋转的性质即可求解.
(2)根据(1)①中的步骤进行证明即可.
(3)
解:(1)①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=ED,![]()
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,

∴△ABE≌△CBD(SAS),
∴AE=CD,∠BAE=∠BCD,
由三角形的外角性质,∠AOC=∠BAE+∠BDC=∠BCD+∠BDC,
∠ABC=∠BCD+∠BDC,
∴∠AOC=∠ABC=![]() ;
;

故答案为:![]() ;
;![]() .
.
②![]() 可看作由
可看作由![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的(或
得到的(或![]() 可看作由
可看作由![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到)
得到)
(2)依然成立,理由如下:
∵![]() 和
和![]() 均是等边三角形,
均是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]()
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
设![]() 与
与![]() 交于点
交于点![]()
∵![]() ,
,
∴![]()
在![]() 和
和![]() 中,其内角和均为
中,其内角和均为![]()
∵![]() ,
,
∴![]()
(3)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,
,
根据旋转的性质可得:![]()
![]()
![]()
![]()
![]()

![]()


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段![]() 的两个端点均在小正方形的顶点上.
的两个端点均在小正方形的顶点上.

(1)如图①,点![]() 在小正方形格点上,在图①中作出点
在小正方形格点上,在图①中作出点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,并直接写出四边形
,并直接写出四边形![]() 的周长;
的周长;
(2)在图②中画出一个以线段![]() 为一条对角线、面积为15的菱形
为一条对角线、面积为15的菱形![]() ,且点
,且点![]() 和点
和点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)求直线AB的表达式;
(2)求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
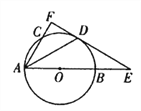
(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,AB=AD,点E在边BC上,∠C=∠AED,AB与DE交于点O.

(1)求证:△ABC≌△ADE;
(2)当∠1=40°时,求∠BED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小慧从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需要将方向调整到与出发时一致,则方向的调整应为( )

A.左转80°B.右转80°C.左转100°D.右转100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com