
 如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号)
如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号) 分析 利用正切的定义分别在两个直角三角形中有AB表示出BD和BC,然后利用BC-BD=8列方程,再解关于AB的方程即可.
解答 解:在Rt△ABD中,∵tan∠ADB=$\frac{AB}{BD}$,
∴BD=$\frac{AB}{tan60°}$=$\frac{AB}{\sqrt{3}}$,
在Rt△ACB中,∵tan∠ACB=$\frac{AB}{BC}$,
∴BC=$\frac{AB}{tan30°}$=$\frac{AB}{\frac{\sqrt{3}}{3}}$=$\frac{3AB}{\sqrt{3}}$,
∵BC-BD=8,
∴$\frac{3AB}{\sqrt{3}}$-$\frac{AB}{\sqrt{3}}$=8,
∴AB=4$\sqrt{3}$(m).
答:树高AB为4$\sqrt{3}$米.
点评 本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.平行投影中物体与投影面平行时的投影是全等的.


科目:初中数学 来源: 题型:填空题
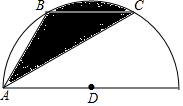 某工件形状如图(阴影部分),圆弧BC的度数为60°,且BC∥AD,BC=6cm,求阴影的面积.
某工件形状如图(阴影部分),圆弧BC的度数为60°,且BC∥AD,BC=6cm,求阴影的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:填空题
关于x的一元二次方程(m-1)x2+x+m2-1=0的一个根为0,则m的值为__________
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{2}{3}}$xyz与$\sqrt{\frac{2}{3}}$xy是同类项 | B. | $\frac{1}{x}$和2x是同类项 | ||
| C. | -0.5x3y2和2x2y3是同类项 | D. | 5m2n和-2nm2是同类项 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
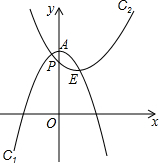 如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).
如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com