
【题目】近一周,各个学校均在紧张有序的进行中考模拟考试,学生们通过模拟考试来调整自己的状态并了解自己的学业水平.某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数,在全年级随机抽取了男、女各40名学生的成绩,并将数据进行整理分析,给出了下面部分信息:
①男生成绩扇形统计图和女生成绩频数分布直方图如下:(数据分组为A组:x<50,B组:50≤x<60,C组:60≤x<70,D组:70≤x≤80)
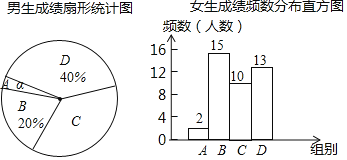
②男生C组中全部15名学生的成绩为:63,69,64,62,68,69,65,69,65,66,67,61,67,66,69
③两组数据的平均数、中位数、众数、满分率、极差(单位:分)如表所示:
平均数 | 中位数 | 众数 | 满分率 | 极差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
(1)扇形统计图A组学生对应的圆心角α的度数为______.
(2)若成绩在70分(包含70分)以上为优秀,请你估计该校1200名学生此次考试中优秀的人数.
科目:初中数学 来源: 题型:
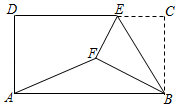
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高尔基说:“书,是人类进步的阶梯. ”阅读可以丰富知识、拓展视野、充实生活等诸多益处. 为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
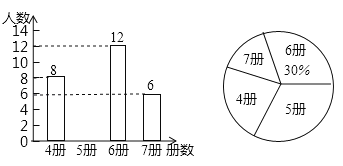
(1)条形图中丢失的数据是 ,并写出阅读书册数的众数是 、中位数是 ;
(2)根据随机抽查的这个结果,估计该校1200名学生中课外阅读5册书的学生人数是 ;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
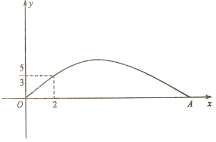
【题目】在某场足球比赛中,球员甲在球门正前方点O处起脚射门,在不受阻挡的情况下,足球沿如图所示的抛物线飞向球门中心线,当足球飞行的水平距离为2 m时,高度为![]() ,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
(1)飞行的足球能否射入球门?通过计算说明理由;
(2)若守门员乙站在球门正前方2 m处,他跳起时能摸到的最大高度为2.52 m,他能阻止此次射门吗?并写明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
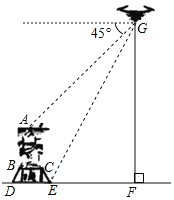
【题目】为了测量重庆有名的观景点南山大金鹰的大致高度,小南同学使用的无人机进行观察,当无人机与大金鹰侧面在同一平面,且距离水平面垂直高度GF为100米时,小南调整摄像头方向,当俯角为45°时,恰好可以拍摄到金鹰的头顶A点;当俯角为63°时,恰好可以拍摄到金鹰底座点E.已知大金鹰是雄踞在一人造石台上,石台侧面CE长12.5米,坡度为1:0.75,石台上方BC长10米,头部A点位于BC中点正上方.则金鹰自身高度约( )米.(结果保留一位小数,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
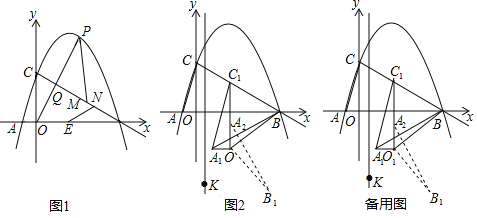
(1)如图1,当![]() 值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
(2)如图2,连接AC,将△AOC沿射线CB方向平移,点A,C,O平移后的对应点分别记作A1,C1,O1,当C1B=O1B时,连接A1B、O1B,将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=![]() 上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
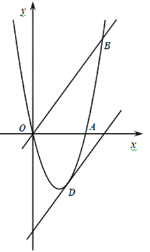
【题目】如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)求抛物线解析式.
(2)将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务:
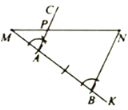
我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使![]() .
.
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使![]() ,连接BN;
,连接BN;
③作射线![]() ,交MN于点P点P即为所求作的点.
,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵![]() (作法),∴
(作法),∴![]()
∵![]() (已知),
(已知),![]() (等量代换)
(等量代换)
∵![]() (线段和差定义),∴
(线段和差定义),∴![]() (等量代换,等式性质)
(等量代换,等式性质)
数学思考:(1)小颖作法理由中所缺的依据是:________________________________.
拓展应用:(2)如图,已知线段a,b,c,求作线段d,使![]()
a. ![]() b.
b. ![]() c.
c. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4![]() ;
;
②S△AED=![]() S四边形ABCD;
S四边形ABCD;
③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com