Question

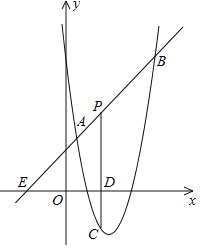
【题目】如图，直线与抛物线相交于和，点P是线段AB上异于A、B的动点，过点P作轴于点D，交抛物线于点C．

求抛物线的解析式；

是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；

连接AC，直接写出为直角三角形时点P的坐标．

Answer 1

【答案】（1）；（2）当时，线段PC最大且为；（3）为直角三角形时，点P的坐标为或

【解析】

(1)已知B(4，m)在直线y=x+2上，可求得m的值，抛物线图象上的A、B两点坐标，可将其代入抛物线的解析式中，通过待定系数法即可求得解析式；

(2)设出P点横坐标，根据直线AB和抛物线的解析式表示出P、C的纵坐标，进而得到关于PC与P点横坐标的函数关系式，化成顶点式即可；

(3)当△PAC为直角三角形时，根据直角顶点的不同，有三种情形，需要分类讨论，分别求解．

在直线上，

，

，

，在抛物线上，

，解得，

抛物线的解析式为；

设动点P的坐标为，则C点的坐标为，

，

，

，

，

当时，线段PC最大且为；

为直角三角形，

若点P为直角顶点，则，

由题意易知，轴，，因此这种情形不存在；

若点A为直角顶点，则，

如图1，过点作轴于点N，则，，

过点A作直线AB，交x轴于点M，则由题意易知，为等腰直角三角形，

，

，

，

设直线AM的解析式为：，

则：，解得，

直线AM的解析式为：，

又抛物线的解析式为：，

联立式，解得：或与点A重合，舍去，

，即点C、M点重合，

当时，，

；

若点C为直角顶点，则．

，

抛物线的对称轴为直线，

如图2，作点关于对称轴的对称点C，

则点C在抛物线上，且，

当时，，

，

点、均在线段AB上，

综上所述，为直角三角形时，点P的坐标为或