
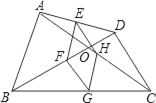
【题目】①如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.
(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论;
②如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC,交CE的延长线与点F.求证:AB垂直平分DF.
【答案】①(1)见解析;(2)见解析; ②见解析.
【解析】
①(1)由三角形中位线知识可得EF=GH,EF∥GH,继而可得四边形EFGH是平行四边形;
(2)要是菱形,只需增加相邻两边相等,如要得到EF=GF,由中位线知识,只须AB=CD.
②由FB∥AC,∠ACB=90°可得∠FBC=90°,继而可得∠DBA=45°,通过证明Rt△ADC≌Rt△FBC,可得DB=FB,继而可证得答案.
①(1)∵E、F分别是AD、BD中点,
∴EF∥AB,EF=![]() AB,
AB,
同理GH∥AB,GH=![]() AB,
AB,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD满足AB=CD时,四边形EFGH是菱形,证明如下:
∵F、G分别是BD、BC中点,∴GF=![]() CD,
CD,
∵AB=CD,∴EF=GF,
又∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形;

②∵∠ACB=90°,Rt△ADC中,∠1+∠2=90°,
∵AD⊥CF,在Rt△EDC中,∠3+∠2=90°,得:∠1=∠3,
∵FB∥AC,∠ACB=90°,∴∠FBC=90°,得:△FBC是直角三角形,
∵AC=BC,∠1=∠3,△FBC是直角三角形,
∴Rt△ADC≌Rt△FBC,
∴CD=FB,∵CD=DB,∴DB=FB,
∵AC=BC、∠ACB=90°,∴∠4=45°,∴AB是∠CBF平分线,
所以,AB垂直平分DF(等腰三角形中的三线合一定理).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为CD上一点,连接AE,BD,且AE,BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )
A.4:25
B.4:9
C.9:25
D.2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3b|+(a+b-4)=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
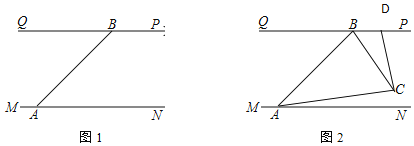
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )

A. (![]() ,
,![]() )B. (2,
)B. (2,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,3﹣
,3﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
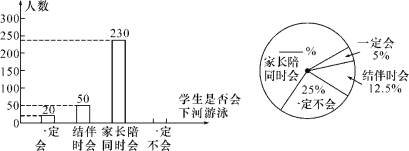
(1)这次抽样调查中,共调查了__ __名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.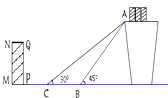
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物 ![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,P为对角线BD上任意一点,连接PA、PC,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论:①S1=S2;②S1+S2=S3;③S1+S3=S2+S4;④若S1S3=S2S4 , 其中正确结论的序号是 . (在横线上填上你认为所有正确答案的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com