练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

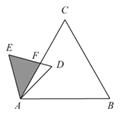
    【题目】如图，已知△ABC是面积为的等边三角形，△ABC∽△ADE，AB＝2AD，∠BAD＝45°，AC与DE相交于点F，则△AEF的面积等于 （结果保留根号）．

    【答案】．

    【解析】

    试题∵AB=2AD，

    ∴=2，

    又∵△ABC∽△ADE，△ABC是面积为，

    ∴=4，

    ∴S△ADE=，

    ∵△ABC∽△ADE，△ABC是等边三角形，

    ∴△ADE也是等边三角形，其面积为AE2=，

    ∴AE=1，

    作FG⊥AE于G，

    ∵∠BAD=45°，∠BAC=∠EAD=60°，

    ∴∠EAF=45°，

    ∴△AFG是等腰直角三角形，

    设AG=FG=h，在直角三角形FGE中，

    ∵∠E=60°，EG=1﹣h，FG=h，

    ∴tan∠E=，即tan60°=，解得h=，

    ∴S△AEF=×1×=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

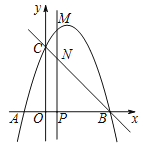
    【题目】如图，抛物线与轴交于、两点（点在点的左侧），点的坐标为，与轴交于点，作直线．动点在轴上运动，过点作轴，交抛物线于点，交直线于点，设点的横坐标为．

    （Ⅰ）求抛物线的解析式和直线的解析式；

    （Ⅱ）当点在线段上运动时，求线段的最大值；

    （Ⅲ）当以、、、为顶点的四边形是平行四边形时，直接写出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

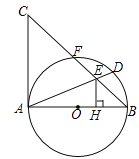
    【题目】如图，已知AB为⊙O直径，AC是⊙O的切线，连接BC交⊙O于点F，取的中点D，连接AD交BC于点E，过点E作EH⊥AB于H．

    （1）求证：△HBE∽△ABC；

    （2）若CF=4，BF=5，求AC和EH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

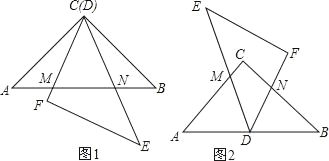
    【题目】小明将两个全等的等腰三角板摆放在一起，其中∠ACB＝∠DFE＝90°，AB＝DE＝12．

    （1）如图1，当D与C点重合时，CF、CE分别与AB交于M、N两点，且量得AM＝3，BN＝4，小明发现AM、MN、BN存在某种数量关系，他想：当AM＝a，BN＝b，MN＝c时，这种数量关系仍成立吗？请你一起探究并证明这个结论；

    （2）如图2，当等腰Rt△DEF的顶点D恰好在AB的中点处时，DE、DF分别与AC、BC交于M、N，小明经测量后猜想，AMBN是一个定值．你认可他的猜想吗？说明理由，若猜想成立，请求出该定值．

    （3）在（2）的条件下，△DEF绕点D旋转，DE、DF所在的直线分别交线段AC和线段BC于点M、N，若CN＝2，求MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC于点E，交BC于点D．求证：

    （1）D是BC的中点；

    （2）△BEC∽△ADC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的袋子里装有红、黄、蓝三种颜色的球（除颜色以外，其余都相同），其中红球2个，黄球2个，从中随机摸出一个球是蓝色球的概率为 ．

    （1）求袋子里蓝色球的个数；

    （2）甲、乙两人分别从袋中摸出一个球（不放回），求摸出的两个球中一个是红球一个是黄球的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

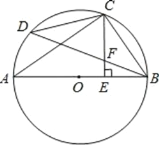
    【题目】如图，AB 是⊙O 的直径，C 是的中点，CE⊥AB 于点 E，BD 交CE 于点 F．

    (1)求证：CF＝BF；

    (2)若 CD＝6，AC＝8，求⊙O 的半径及 CE 的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用适当的方法解方程

    （1）2x2﹣5x﹣3＝0

    （2）（2x﹣5）2＝4（2x﹣5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程x2＋（m－2）x＋m＋1=0有两个相等的实数根，则m的

    值是

    A. 0 B. 8 C. 4±2 D. 0或8

    查看答案和解析>>

    同步练习册答案