
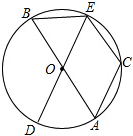
 如图,AB、DE是⊙O的直径,C是⊙O上的一点,且
如图,AB、DE是⊙O的直径,C是⊙O上的一点,且 |
| AD |
 |
| CE |
科目:初中数学 来源: 题型:
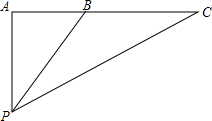 为制作一部海洋专题片,一摄像师在一直升飞机上进行航拍,飞机在同一高度沿一条直线飞行,飞机每秒钟飞行20米.当飞机飞到A点时,摄像师发现自己的正下方的海面上有一美丽景色P,一段时间后飞机飞到B点,此时测得其俯角是35.1°,又经过了半分钟,飞机飞到C点,此时测得此俯角是16.8°,由此你能知道飞机的大约高度吗?(参考数据:sin35.1°=0.58,cos35.1°=0.82,tan35.1°=0.70,sin16.8°=0.29,cos16.8°=0.96,tan16.8°=0.30)
为制作一部海洋专题片,一摄像师在一直升飞机上进行航拍,飞机在同一高度沿一条直线飞行,飞机每秒钟飞行20米.当飞机飞到A点时,摄像师发现自己的正下方的海面上有一美丽景色P,一段时间后飞机飞到B点,此时测得其俯角是35.1°,又经过了半分钟,飞机飞到C点,此时测得此俯角是16.8°,由此你能知道飞机的大约高度吗?(参考数据:sin35.1°=0.58,cos35.1°=0.82,tan35.1°=0.70,sin16.8°=0.29,cos16.8°=0.96,tan16.8°=0.30)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com