
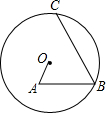
 如图所示,在⊙O内有折线OABC,其中OA=4,AB=6,∠A=∠B=60°,则BC的长为10.
如图所示,在⊙O内有折线OABC,其中OA=4,AB=6,∠A=∠B=60°,则BC的长为10. 分析 首先延长AO交BC于D,作OH⊥BC于H,由∠A=∠B=60°,可判断△ABD为等边三角形,根据等边三角形的性质可求得BD的长,再由含30°角的直角三角形的性质,求得DH的长,则可得到BH的长,根据垂径定理的性质,即可求得答案.
解答 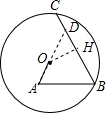 解:延长AO交BC于D,作OH⊥BC于H,
解:延长AO交BC于D,作OH⊥BC于H,
∵∠A=∠B=60°,
∴△ABD为等边三角形,
∴∠ADB=60°,AD=BD=AB=6,
∴OD=AD-OA=6-4=2,
在Rt△ODH中,∠ODH=60°,
∴∠DOH=30°,
∴DH=$\frac{1}{2}$OD=1,
∴BH=BD-DH=6-1=5,
∵OH⊥BC,
∴BC=2BH=10.
故答案为:10.
点评 本题考查了垂径定理、等边三角形的判定与性质以及含30°角的直角三角形的性质.注意准确作出辅助线是解此题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知四个数:a=(-2)2,b=-|-2|,c=-(-1)2016,d=-(-3).
已知四个数:a=(-2)2,b=-|-2|,c=-(-1)2016,d=-(-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com