
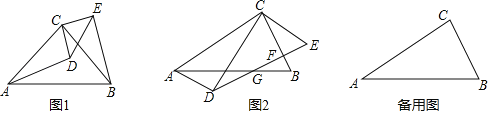
【题目】在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,AB=CF.
(1)如图1,求证:DF=DB;
(2)如图2,若AF=![]() DF,在不添加任何辅助线和字母的情况下,请写出图中所有度数与3∠FAE的度数相等的角.
DF,在不添加任何辅助线和字母的情况下,请写出图中所有度数与3∠FAE的度数相等的角.

【答案】(1)证明见解析;(2)∠CAB,∠ABC,∠DFC,∠AFE与3∠FAE的度数相等,理由见解析.
【解析】
(1)由余角的性质可得∠DAB=∠DCE,由“AAS”可证△ADB≌△CDF,可得DF=BD;
(2)由等腰三角形的性质可求∠DFB=∠DBF=45°,即可求∠ABD=∠DBF+∠ABF=67.5°,由全等三角形的性质可得∠CAB=∠DCF=∠ABD=∠AFE=67.5°=3∠FAE.
(1)∵AD⊥BC,CE⊥AB
∴∠B+∠DAB=90°,∠B+∠DCE=90°
∴∠DAB=∠DCE,且∠ADB=∠ADC=90°,CF=AB
∴△ADB≌△CDF(AAS)
∴DF=BD
(2)∠CAB,∠ABC,∠DFC,∠AFE与3∠FAE的度数相等,
理由如下:如图:连接BF,

∵DF=DB,∠ADB=90°
∴∠DFB=∠DBF=45°,BF=![]() DF,且AF=
DF,且AF=![]() DF
DF
∴AF=BF
∴∠FAE=∠FBE
∴∠DFB=2∠FAE=2∠ABF=45°
∴∠FAE=∠FBE=22.5°
∴∠ABD=∠DBF+∠ABF=67.5°
∴∠ABD=3∠FAE
∵△ADB≌△CDF
∴∠DCF=∠ABD=∠AFE=67.5°=3∠FAE,
AD=CD
∴∠DAC=∠DCA=45°
∴∠CAB=67.5°=3∠FAE


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )
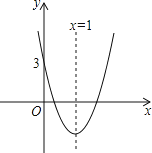
A. ②③④B. ①②③C. ②③D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
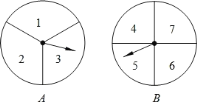
【题目】甲、乙两人用如图的两个分格均匀的转盘![]() 做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:求甲、乙两人获胜的概率.
做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,侧得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC为( )
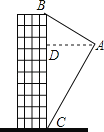
A. 90+30![]() B. 90+60
B. 90+60![]() C. 90+90
C. 90+90![]() D. 90+180
D. 90+180![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为( )

A. 5B. 6C. 8D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
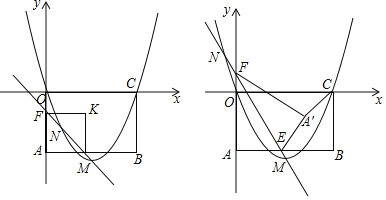
【题目】矩形OABC的边OC、OA分别位于x、y轴上,点A(0,﹣4)、B(6,﹣4)、C(6,0),抛物线y=ax2+bx经过点O和点C,顶点M(3,﹣![]() ),点N是抛物线上一动点,直线MN交直线AB于点E,交y轴于F,△A′EF是将△AEF沿直线MN翻折后的图形.
),点N是抛物线上一动点,直线MN交直线AB于点E,交y轴于F,△A′EF是将△AEF沿直线MN翻折后的图形.
(1)求抛物线的解析式;
(2)当四边AEA′F是正方形时,求点N的坐标.
(3)连接CA′,求CA′的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)△ABC和△CDE是两个等腰直角三角形,如图1,其中∠ACB=∠DCE=90°,连结AD、BE,求证:△ACD≌△BCE.
(2)△ABC和△CDE是两个含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE从边CD与AC重合开始绕点C逆时针旋转一定角度α(0°<α<180°);
①如图2,DE与BC交于点F,与AB交于点G,连结AD,若四边形ADEC为平行四边形,求![]() 的值;
的值;
②若AB=10,DE=8,连结BD、BE,当以点B、D、E为顶点的三角形是直角三角形时,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com