
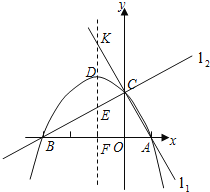
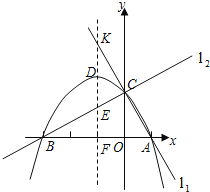
【题目】已知两直线l1,l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1,抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
【答案】(1)抛物线的函数解析式为![]() ;(2)截得三条线段的数量关系为KD=DE=EF.理由见解析;(3)当点M的坐标分别为(﹣2,
;(2)截得三条线段的数量关系为KD=DE=EF.理由见解析;(3)当点M的坐标分别为(﹣2,![]() ),(﹣1,
),(﹣1,![]() )时,△MCK为等腰三角形.
)时,△MCK为等腰三角形.
【解析】
解:(1)∵l1⊥l2,
∴∠ACB=90°,即∠ACO+∠BCO=90°,
又∠ACO+∠CAO=90°,
∴∠BCO=∠CAO,又∠COA=∠BOC=90°
∴△BOC∽△COA,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴点C的坐标是(0,![]() ),
),
由题意,可设抛物线的函数解析式为![]() ,
,
把A(1,0),B(﹣3,0)的坐标分别代入![]() ,
,
得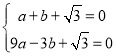 ,
,
解这个方程组,得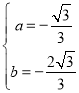 ,
,
∴抛物线的函数解析式为![]() .
.
(2)截得三条线段的数量关系为KD=DE=EF.
理由如下:
可求得直线l1的解析式为![]() ,直线l2的解析式为
,直线l2的解析式为![]() ,
,
抛物线的对称轴为直线x=-1,
由此可求得点K的坐标为(﹣1,![]() ),
),
点D的坐标为(﹣1,![]() ),点E的坐标为(﹣1,
),点E的坐标为(﹣1,![]() ),点F的坐标为(﹣1,0),
),点F的坐标为(﹣1,0),
∴KD=![]() ,DE=
,DE=![]() ,EF=
,EF=![]() ,
,
∴KD=DE=EF.
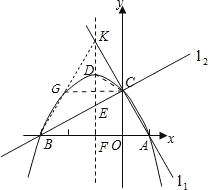
(3)当点M的坐标分别为(﹣2,![]() ),(﹣1,
),(﹣1,![]() )时,△MCK为等腰三角形.
)时,△MCK为等腰三角形.
理由如下:
(i)连接BK,交抛物线于点G,易知点G的坐标为(﹣2,![]() ),
),
又∵点C的坐标为(0,![]() ),则GC∥AB,
),则GC∥AB,
∵可求得AB=BK=4,且∠ABK=60°,即△ABK为正三角形,
∴△CGK为正三角形
∴当l2与抛物线交于点G,即l2∥AB时,符合题意,此时点M1的坐标为(﹣2,![]() ),
),
(ii)连接CD,由KD=![]() ,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形,
,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形,
∴当l2过抛物线顶点D时,符合题意,此时点M2坐标为(﹣1,![]() ),
),
(iii)当点M在抛物线对称轴右边时,只有点M与点A重合时,满足CM=CK,
但点A、C、K在同一直线上,不能构成三角形,
综上所述,当点M的坐标分别为(﹣2,![]() ),(﹣1,
),(﹣1,![]() )时,△MCK为等腰三角形.
)时,△MCK为等腰三角形.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b(k≠0)的图象经过A(3,18)和B(﹣2,8)两点.
(1)求一次函数的解析式;
(2)若一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象只有一个交点,求交点坐标.
(m≠0)的图象只有一个交点,求交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在校园艺术节期间举行学生书画大赛活动,准备购买甲、乙两种文具,奖励在活动中表现优秀的学生.已知购买2个甲种文具、1个乙种文具共需花费35元;购买1个甲种文具、3个乙种文具共需花费30元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共120个,投入资金不少于95元又不多于1000元,问有多少种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
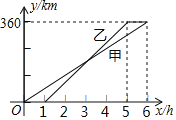
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲,y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h;
(2)当1≤x≤5时,求y乙关于x的函数关系式;
(3)当乙与A地相距240km时,直接写出甲与A地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
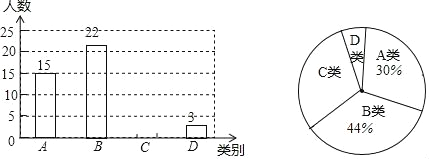
【题目】某校为了解本校九年级学生物理实验操作技能考查的备考情况,随机抽取该年级部分学生进行了一次测试,并根据中考标准按测试成绩分成A、B、C、D四个等级,绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次抽取参加测试的学生为_____人,扇形统计图中A等级所对的圆心角是____度;
(2)请补全条形统计图和扇形统计图;
(3)若该校九年级男生有300人,请估计该校九年级学生物理实验操作成绩为C等级的有____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习网站针对疫情停课不停学推出了套餐优惠服务:已知购买2个学习账号和1个错题伴印设备需要2700元,购买3个学习账号和2个错题伴印设备需要4800元.

(1)求1个学习账号和1个错题伴印设备的单价各是多少元?
(2)若某学习小组准备购买账号和错题伴印设备共45个,且要求伴印设备不低于账号数量的![]() ,请问如何购买才能使得总费用最低,最低费用为多少?
,请问如何购买才能使得总费用最低,最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
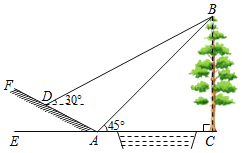
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(![]() ≈1.732,结果精确到0.1)
≈1.732,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
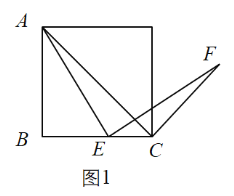
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法,下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.
问题情境:在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() 为边
为边![]() 上一点,连接
上一点,连接![]() .以
.以![]() 为旋转中心,将线段
为旋转中心,将线段![]() 顺时针旋转,旋转角与
顺时针旋转,旋转角与![]() 相等,得到线段
相等,得到线段![]() ,连接
,连接![]() .
.
(1)特例如图1,若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 位置关系是_________.此时可以过点
位置关系是_________.此时可以过点![]() 作
作![]() 的平行线来对结论进行证明(这里不要求证明)
的平行线来对结论进行证明(这里不要求证明)
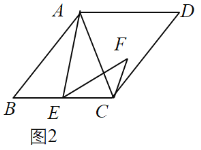
(2)拓展探究:如图2,若四边形![]() 是菱形,当
是菱形,当![]() 时,求
时,求![]() 的度数;
的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com