
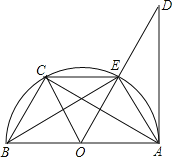
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是![]() 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由C为弧EB中点,利用垂径定理的逆定理得到OC垂直于BE,根据等弧对等弦得到BC=EC,再由AB为直角,利用圆周角定理得到AE垂直于BE,进而得到一对直角相等,利用同位角相等两直线平行得到OC与AE平行,由AD为圆的切线,利用切线的性质得到AB与DA垂直,利用同角的余角相等得到∠DAE=∠ABE,根据E不一定为弧AC中点,可得出AC与OE不一定垂直,即可确定出结论成立的序号.
解:∵C为![]() 的中点,即
的中点,即![]() ,
,
∴OC⊥BE,BC=EC,选项②正确;
设AE与CO交于F,∴∠BFO=90°,
∵AB为圆O的直径,
∴AE⊥BE,即∠BEA=90°,
∴∠BFO=∠BEA,
∴OC∥AE,选项①正确;
∵AD为圆的切线,
∴∠DAB=90°,即∠DAE+∠EAB=90°,
∵∠EAB+∠ABE=90°,
∴∠DAE=∠ABE,选项③正确;
点E不一定为![]() 中点,故E不一定是
中点,故E不一定是![]() 中点,选项④错误,
中点,选项④错误,
则结论成立的是①②③,
故选:C.


科目:初中数学 来源: 题型:
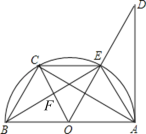
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
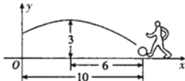
(1)如图建立直角坐标系,当球飞行的路线为一抛物线时,求此抛物线的解析式.
(2)已知球门高为2.44米,问此球能否射中球门(不计其它情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
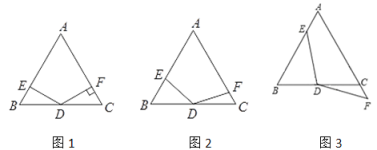
(1)如图1,若DF⊥AC,垂足为F,证明:DE=DF
(2)如图2,将∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.DE=DF仍然成立吗?说明理由.
(3)如图3,将∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,DE=DF仍然成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,龙岗区家庭轿车的拥有量逐年增加.据统计,某小区2017年底拥有家庭轿车81辆,2019年底家庭轿车的拥有量达到144辆.
(1)若该小区2017年底到2019年底家庭轿车拥有量的年平均增长率都相同,求该小区到2020年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资25万元再建造若干个停车位.据测算,建造费用分别为室内车位6000元/个,露天车位2000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的3倍,但不超过室内车位的4.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向上平移3个单位长度,画出平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕B1逆时针旋转90°,画出旋转后的△A2B1C2,求线段B1C1旋转过程中扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△DEF中,EF=10,DF=6,DE=8,以EF的中点O为圆心,作半圆与DE相切,点A、B分别是半圆和边DF上的动点,连接AB,则AB的最大值与最小值的和是( )

A.6B.2![]() +1C.
+1C.![]() D.9
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.

(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假快要到了,某市准备组织同学们分别到A,B,C,D四个地方进行夏令营活动,前往四个地方的人数如图所示.
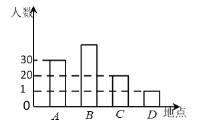
(1)去B地参加夏令营活动人数占总人数的40%,根据统计图求去B地的人数?
(2)若一对姐弟中只能有一人参加夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.用列表法或树形图分析这种方法对姐弟俩是否公平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com