
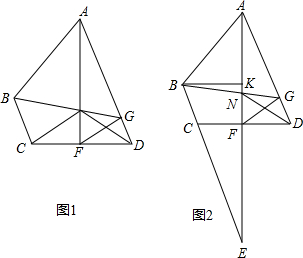
分析 (1)由角平分线得出∠NFG=∠GFD,由SAS证明△GFN≌△GFD即可;
(2)连接AC,由等腰直角三角形的性质得出∠FDN=45°,由线段垂直平分线的性质得出AC=AD,证出∠CAD=30°,由SAS证明△ADN≌△ACB,得出对应边相等即可;
(3)取AB中点H,连接HF、HK,由直角三角形斜边上的中线性质得出HK=$\frac{1}{2}$AB=AH,得出∠HAK=∠HKA,证明△AFD∽△EFC,得出对应边成比例,证出AF=EF,证明HF为△ABE的中位线,由三角形中位线定理得出HF∥BE,得出∠HFK=∠E,由角的关系得出∠HFK=∠FHK,得出HK=KF,即可得出结论.
解答 (1)证明:∵FG平分∠AFD,
∴∠NFG=∠GFD,
在△GFN和△GFD中,$\left\{\begin{array}{l}{FN=FD}\\{∠NFG=∠GFD}\\{FG=FG}\end{array}\right.$,
∴△GFN≌△GFD(SAS);
(2)证明:连接AC,如图1所示: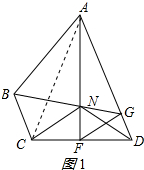
∵AF⊥CD,FN=FD,
∴△DFN为等腰直角三角形,
∴∠FDN=45°,
∵∠ADC=75°,
∴∠ADN=∠ADC-∠FDN=75°-45°=30°,
在Rt△AFD中,∠FAD=90°-75°=15°
∵AF垂直平分CD,
∴AC=AD,
∴∠ACD=∠ADC=75°,
∴∠CAD=30°,
∵AD∥BC,
∴∠BCA=∠CAD=30°,
∴∠ADN=∠BCA,
在△ADN和△ACB中,$\left\{\begin{array}{l}{ND=BC}\\{∠ADN=∠BCA}\\{AD=AC}\end{array}\right.$,
∴△ADN≌△ACB(SAS),
∴AN=AB;
(3)解:AB与KF之间有何数量关系为:AB=2KF;理由如下:
取AB中点H,连接HF、HK,如图2所示: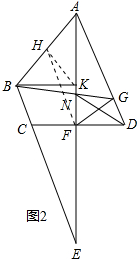
∵在Rt△AKB中,H为AB中点,
∴HK=$\frac{1}{2}$AB=AH,
∴∠HAK=∠HKA,
∵∠BAF=2∠E,
∴∠HKA=2∠E,
∵AD∥BE,
∴△AFD∽△EFC,
∴$\frac{AF}{EF}$=$\frac{DF}{CF}$=1,
∴AF=EF,
∵H为AB中点,
∴HF为△ABE的中位线,
∴HF∥BE,
∴∠HFK=∠E,
∴∠HKA=2∠HFK,
∵∠HKA=∠HFK+∠FHK,
∴2∠HFK=∠HFK+∠FHK,
∴∠HFK=∠FHK,
∴HK=KF,
∵HK=$\frac{1}{2}$AB,
即AB=2HK,
∴AB=2KF.
点评 本题是四边形综合题目,考查了全等三角形的判定与性质、线段垂直平分线的性质、相似三角形的判定与性质、三角形中位线定理、等腰三角形的性质、直角三角形斜边上的中线性质等知识;本题综合性强,难度较大,特别是(2)和(3)中,需要通过作辅助线证明三角形全等,运用三角形中位线定理和直角三角形斜边上的中线性质才能得出结论.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
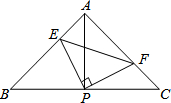 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
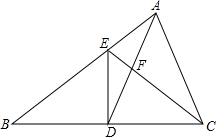 如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=13 | B. | (x-3)2=5 | C. | (x-6)2=13 | D. | (x-6)2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
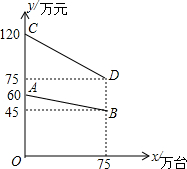 某装备企业采用订单式生产销售某种产品,保证其销售量与产量相等,图中的线段AB,线段CD分别表示该产品每万台生产成本y1(单位:万元)、销售价y2(单位:万元)与产量x(单位:台)之间的函数关系,考虑企业的经济效益,当此种产品市场预定生产为75万台时,将停止订单生产销售,求当该产品产量为多少万台时,可实现2000万元利润?
某装备企业采用订单式生产销售某种产品,保证其销售量与产量相等,图中的线段AB,线段CD分别表示该产品每万台生产成本y1(单位:万元)、销售价y2(单位:万元)与产量x(单位:台)之间的函数关系,考虑企业的经济效益,当此种产品市场预定生产为75万台时,将停止订单生产销售,求当该产品产量为多少万台时,可实现2000万元利润?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com