
【题目】若直角三角形的二条边分别为3cm和4cm,那么它的内切圆则球的半径为_____
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】浙北商场一专柜销售某种品牌的玩具,每件进价为20元.销售过程中发现,每月销售![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系可近似的看作一次函数:
(元)之间的关系可近似的看作一次函数:![]() .
.
(1)若每月销售260件,则每件利润是多少?
(2)如果该专柜想要每月获得2160元的利润,且成本要低.那么销售单价应定为多少元?
(3)设专柜每月获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润多少元?
(元),当销售单价定为多少元时,每月可获得最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
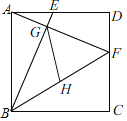
【题目】已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:已知方程![]() ,
,![]() 且
且![]() ,求
,求![]() 的值.
的值.
解:由![]() ,及
,及![]() ,可知
,可知![]() ,
,![]() .
.
又![]()
![]() ,
,
![]() .
.
![]()
![]() 可变形为
可变形为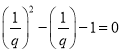 ,
,
根据![]() 和
和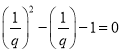 的特征.
的特征.
![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,
的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:![]() ,
,![]() 且
且![]() ,
,
(1)求:![]() 的值.
的值.
(2)求:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
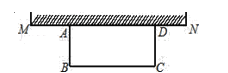
【题目】如图,某农场老板准备建造一个矩形养兔场ABCD,他打算让矩形养兔场的一边完全靠着墙MN,墙MN可利用的长度为24米,另外三边用长度为50米的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分).
(1)若要使矩形养兔场的面积为300平方米,则垂直于墙的一边长AB为多少米?
(2)该矩形养兔场ABCD的面积有最大值吗?若有最大值,请求出面积最大时AB的长度;若没有最大值,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
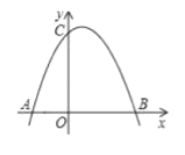
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在
在![]() 轴的右侧且点
轴的右侧且点![]() 在点
在点![]() 的左侧,与
的左侧,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到点
得到点![]() ,直线
,直线![]() 交抛物线的另一个交点为
交抛物线的另一个交点为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)为120万元,在销售过程中发现,年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
⑴ 直接写出![]() 关于
关于![]() 的函数关系式为 .
的函数关系式为 .
⑵ 市场管理部门规定,该产品销售单价不得超过100元,该公司销售该种产品当年获利55万元,求当年的销售单价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次中奖机会.为了活跃气氛.设计了两个抽奖方案:
方案一:转动转盘![]() 一次,转出红色可领取一份奖品;
一次,转出红色可领取一份奖品;
方案二:转动转盘![]() 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
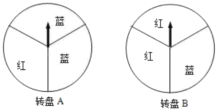
(1)若转动一次![]() 转盘,求领取一份奖品的概率;
转盘,求领取一份奖品的概率;
(2)如果你获得一次抽奖机会,你会选择哪个方案?请采用列表法或树状图说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com