
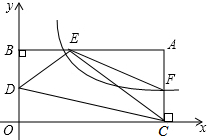
 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
分析 设点E的坐标为(a,b),用a,b表示出图中线段的长,根据矩形和数据线的面积公式以及△DEC的面积为1列出算式,求出ab的值,得到△AEF的面积.
解答 解:设点E的坐标为(a,b),
则OD=BD=$\frac{1}{2}$b,OC=3a,AE=2a,AC=b,
∵△DEC的面积=矩形OCAB的面积-△DOC的面积-△DBE的面积-△AEF的面积,
∴3ab-$\frac{1}{2}$×3a×$\frac{1}{2}$b-$\frac{1}{2}×a×\frac{1}{2}b$-$\frac{1}{2}×2a×b$=1,
∴ab=1,
∴△AEF的面积为:$\frac{1}{2}×2a×b$=1,
故选:D.
点评 本题考查的是反比例函数系数k的几何意义,把y=$\frac{k}{x}$化为k=xy、运用数形结合思想进行解答是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
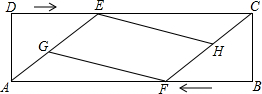 如图,在矩形ABCD中,AB=13cm,AD=4cm,点E、F同时分别从D、B两点出发,以1cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).
如图,在矩形ABCD中,AB=13cm,AD=4cm,点E、F同时分别从D、B两点出发,以1cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
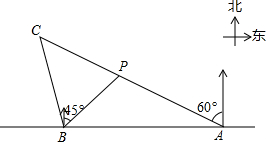 如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.
如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
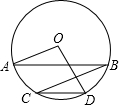 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )| A. | 120° | B. | 140° | C. | 110° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3-x=x(x2-1) | B. | -a2+6a-9=-(a-3)2 | ||
| C. | x2+y2=(x+y)2 | D. | a3-2a2+a=a(a+1)(a-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com