
【题目】如图,直角三角形![]() 与直角三角形
与直角三角形![]() 的斜边在同一直线上,
的斜边在同一直线上,![]() ,
,![]() ,
,![]() 平分
平分![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,记
按逆时针方向旋转,记![]() 为
为![]() ,在旋转过程中:
,在旋转过程中:
(1)如图,当![]() ______时,
______时,![]() ,当
,当![]() ______时,
______时,![]() ;
;
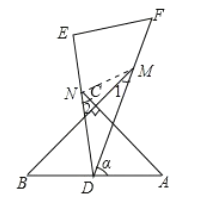
(2)如图,当顶点![]() 在
在![]() 内部时,边
内部时,边![]() 、
、![]() 分别交
分别交![]() 、
、![]() 的延长线于点
的延长线于点![]() 、
、![]() ,记
,记![]() ,
,![]() .
.
①![]() 与
与![]() 度数的和是否变化?若不变,求出
度数的和是否变化?若不变,求出![]() 与
与![]() 度数和;若变化,请说明理由;
度数和;若变化,请说明理由;
②若使得![]() ,求出
,求出![]() 、
、![]() 的度数,并直接写出此时
的度数,并直接写出此时![]() 的度数.
的度数.

【答案】(1)10°,100°;(2)①不变,详见解析;②80°.
【解析】
(1)当∠EDA=∠B=40°时,DE∥BC,得出 30°+α=40°,即可得出结果;当 DE∥AC 时,DE⊥AB,得出 50°+α+30°=180°,即可得出结果;
(2)①连接 MN,由三角形内角和定理得出∠CNM+∠CMN+∠MCN=180°,则∠CNM+∠CMN=90°,由三角形内角和定理得出∠DNM+∠DMN+∠MDN=180°,即∠2+∠CNM+∠CMN+∠1+∠MDN=180°,即可得出结论;②根据①中结论结合本题题意可以得出![]()
![]() 度数,即可求出
度数,即可求出![]() 度数.
度数.
解:(1)∵∠B=40°,
∴当∠EDA=∠B=40°时,DE∥BC, 而∠EDF=30°,
∴30°+α=40°,
解得:α=10°;
当 DE∥AC 时,DE⊥AB, 此时∠A+∠EDA=180°, ∠A=90°-∠B=50°,
∴50°+α+30°=180°, 解得:α=100°;
故答案为 10°,100°;
(2)①∠1 与∠2 度数的和不变;理由如下:
连接 MN,如图所示:
在△CMN 中,∵∠CNM+∠CMN+∠MCN=180°,
∴∠CNM+∠CMN=90°, 在△MND 中,
∵∠DNM+∠DMN+∠MDN=180°, 即∠2+∠CNM+∠CMN+∠1+∠MDN=180°,
∴∠1+∠2=180°-90°-30°=60°.
②∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,点 A( 2,2)、B(0,1)点 P 在 x 轴上,且△PAB 的等腰三角形,则满足条件的点 P 共有()个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的直角顶点C置于直线l上,AC=BC,现过A.B两点分别作直线l的垂线,垂足分别为点D.E.
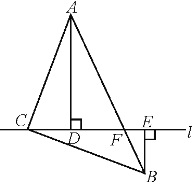
(1)求证:△ACD≌△CBE.
(2)若BE=3,DE=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
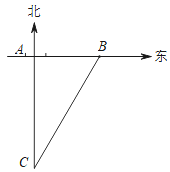
【题目】如图,一艘轮船以30km/h的速度沿既定航线由南向北航行,途中接到台风警报,某台风中心正以10km/h的速度由东向西移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离AB=300km.
(1)如果这艘船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
(3)假设轮船航向不变,轮船航行速度不变,求受到台风影响的时间为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() ABC中,
ABC中,![]() ,
,![]() ,点D是AB中点,
,点D是AB中点,

(1)点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.
(i)求证:△BCD为等边三角形;
(ii)随着点E位置的变化,![]() 的度数是否变化?若不变化,求出
的度数是否变化?若不变化,求出![]() 的度数;
的度数;
(2)DP![]() AB交AC于点P,点E为线段AP上一点,连结BE,作
AB交AC于点P,点E为线段AP上一点,连结BE,作![]() ,如图2所示,EQ交PD延长线于Q,探究线段PE,PQ与AP之间的数量关系,并证明.
,如图2所示,EQ交PD延长线于Q,探究线段PE,PQ与AP之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 箱中装有3张相同的卡片,它们分别写有数字1,2,4;
箱中装有3张相同的卡片,它们分别写有数字1,2,4;![]() 箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从
箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从![]() 箱、
箱、![]() 箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率.
(2)如果取出![]() 箱中卡片上的数字作为十位上的数字,取出
箱中卡片上的数字作为十位上的数字,取出![]() 箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com