
【题目】某个体户购进一批时令水果,20天销售完毕,他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图所示,则下列说法不正确的是( )

A.第10天销售20千克B.一天最多销售30千克
C.第9天与第16天的日销售量相同D.第19天比第1天多销售4千克
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西45°方向,在D处测得栈道另一端B位于北偏东32°方向.已知AC=60 m ,CD=46 m,求栈道AB的长(结果保留整数).参考数据:sin32° ≈ 0.53,cos32° ≈ 0.85,tan32° ≈ 0.62,![]() ≈ 1.414.
≈ 1.414.

查看答案和解析>>
科目:初中数学 来源: 题型:
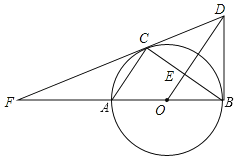
【题目】如图,已知AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是⊙O的切线;
(2)若∠ABC=30°,AB=8,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 自变量
自变量![]() 的值和它对应的函数值
的值和它对应的函数值![]() 如下表所示:
如下表所示:
| … | 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | … |
(1)点M是该二次函数图象上一点,若点M纵坐标为8时,求点M的坐标;
(2)设该二次函数图象与![]() 轴的左交点为
轴的左交点为![]() ,它的顶点为
,它的顶点为![]() ,该图象上点
,该图象上点![]() 的横坐标为4,求
的横坐标为4,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 交于
交于![]() ,B两点,与y轴交于点
,B两点,与y轴交于点![]() .
.
(1)求抛物线的解析式;
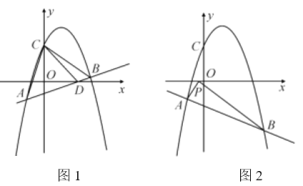
(2)如图1,直线AB交![]() 轴于点D,且
轴于点D,且![]() ,求点B的坐标;
,求点B的坐标;
(3)如图2,当![]() 时,在x轴上有且只有一点P,使
时,在x轴上有且只有一点P,使![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
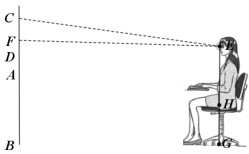
【题目】疫情期间部分学生选择在家用电视观看网络课程,为了保护眼睛,电视机的安装高度有一定的要求.如图所示,小嘉家的壁挂电视机的安装高度![]() 为1米,电视的中心位置
为1米,电视的中心位置![]() (
(![]() 的中点)比平视视线
的中点)比平视视线![]() 低
低![]() (这样观看眼睛最不容易疲劳),电视机宽度
(这样观看眼睛最不容易疲劳),电视机宽度![]() 为
为![]() ,眼到凳子平面的高度
,眼到凳子平面的高度![]() 为
为![]() .
.
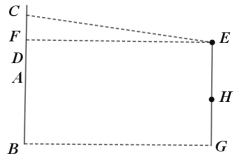
(1)求小嘉应选用凳子的高度;
(2)若看电视的视角![]() 为
为![]() 时,观看感最好,求此时凳子中心
时,观看感最好,求此时凳子中心![]() 到墙
到墙![]() 的距离(电视机的厚度忽略不计).(参考数据:
的距离(电视机的厚度忽略不计).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
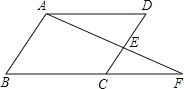
【题目】如图,点E是ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)若AD的长为2.求CF的长.
(2)若∠BAF=90°,试添加一个条件,并写出∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
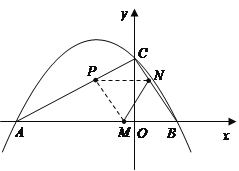
【题目】如图,二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .连结
.连结![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,且当
,且当![]() 和
和![]() 时二次函数的函数值
时二次函数的函数值![]() 相等.
相等.
(1)求实数![]() 的值;
的值;
(2)若点![]() 同时从
同时从![]() 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿![]() 边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为
边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为![]() 秒时,连结
秒时,连结![]() ,将
,将![]() 沿
沿![]() 翻折,
翻折,![]() 点恰好落在
点恰好落在![]() 边上的
边上的![]() 处,求
处,求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(3)在(2)的条件下,二次函数图象的对称轴上是否存在点![]() ,使得以
,使得以![]() 为项点的三角形与
为项点的三角形与![]() 相似?如果存在,请求出点
相似?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com