
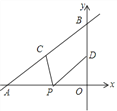
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
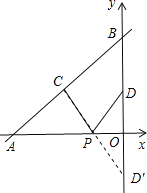
详解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() x+4中y=0,则
x+4中y=0,则![]() x+4=0,解得:x=6,
x+4=0,解得:x=6,
∴点A的坐标为(6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(3,2),D′(0,2),
∴有![]() ,解得:
,解得: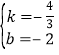 ,
,
∴直线CD′的解析式为y=![]() x2.
x2.
令y=![]() x2中y=0,则0=
x2中y=0,则0=![]() x2,解得:x=
x2,解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
故选C.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
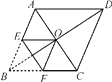
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
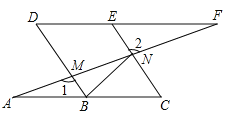
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
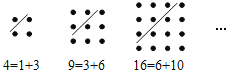
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在钟面上,点![]() 为钟面的圆心,以点
为钟面的圆心,以点![]() 为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
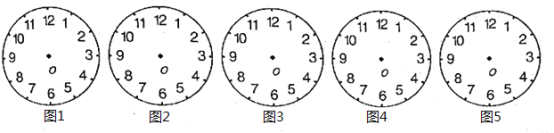
(1)在图1中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图2中画一个直角,使直角的内部含有3个数字,且数字之积等于数字之和;
(3)在图3中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图4中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图5中画两个直角,使这两个直角的内部含有的3个数字之和相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com