
【题目】解方程
(1)解方程: ![]() +
+ ![]() =4.
=4.
(2)解不等式组: ![]() .
.
【答案】
(1)解:去分母得:x﹣5x=4(2x﹣3),
解得:x=1,
经检验x=1是分式方程无解
(2)解: ![]() ,
,
∵由①得,x<2,
由②得,x≥﹣1,
∴不等式组的解集是:﹣1≤x<2
【解析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;(2)首先解每个不等式,两个不等式组的解集的公共部分就是不等式组的解集.
【考点精析】本题主要考查了去分母法和一元一次不等式组的解法的相关知识点,需要掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | … |

(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1 , 当点C1、B1、C三点共线时,旋转角为α,连接BB1 , 交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1 , 其中正确的是( ) 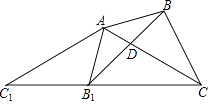
A.①③④
B.①②④
C.②③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+b|(b为常数)的图象.若该图象在直线y=2下方的点的横坐标x满足0<x<3,则b的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 ![]() cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以 ![]() cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x=;
(2)当点M落在AD上时,x=;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA= ![]() ,抛物线y=ax2﹣ax﹣a经过点B(2,
,抛物线y=ax2﹣ax﹣a经过点B(2, ![]() ),与y轴交于点D.
),与y轴交于点D.
(1)求抛物线的表达式;
(2)点B关于直线AC的对称点是否在抛物线上?请说明理由;
(3)延长BA交抛物线于点E,连接ED,试说明ED∥AC的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂对零件进行检测,引进了检测机器.已知一台检测机的工作效率相当于一名检测员的20倍.若用这台检测机检测900个零件要比15名检测员检测这些零件少3小时.
(1)求一台零件检测机每小时检测零件多少个?
(2)现有一项零件检测任务,要求不超过7小时检测完成3450个零件.该厂调配了2台检测机和30名检测员,工作3小时后又调配了一些检测机进行支援,则该厂至少再调配几台检测机才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系: ;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC= 时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com