
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() 在
在![]() 轴上一定点,
轴上一定点,![]() 为
为![]() 轴上一动点,且点
轴上一动点,且点![]() 从原点
从原点![]() 出发,沿着
出发,沿着![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度运动,已知
个单位长度运动,已知![]() 点运动时间为
点运动时间为![]() .
.
(1)点![]() 坐标为________,
坐标为________,![]() 点坐标为________;(直接写出结果,可用
点坐标为________;(直接写出结果,可用![]() 表示)
表示)
(2)当![]() 为何值时,
为何值时,![]() 为等腰三角形;
为等腰三角形;
(3)![]() 点在运动过程中,是否存在
点在运动过程中,是否存在![]() ,使得
,使得![]() ,若存在,请求出
,若存在,请求出![]() 的值,若不存在,请说明理由!
的值,若不存在,请说明理由!

【答案】(1)(4,4),(![]() ,0);(2)1,
,0);(2)1,![]() ,4; (3)存在,
,4; (3)存在,![]()
【解析】
(1)利用平行四边形的性质和根据P点的运动速度,利用路程公式求解即可;
(2)分三种情况:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别讨论求解,即可得出结果;
时,分别讨论求解,即可得出结果;
(3)过D点作![]() 交BP于点F,设
交BP于点F,设![]() ,则可得
,则可得![]() ,
,![]() ,
,![]() ,利用
,利用![]() ,即可求出
,即可求出![]() 的长,利用路程公式可求得
的长,利用路程公式可求得![]() 的值。
的值。
解:(1)∵![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
∴点![]() 坐标为(4,4),
坐标为(4,4),
又∵![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 从原点
从原点![]() 出发,沿着
出发,沿着![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度运动,
个单位长度运动,![]() 点运动时间为
点运动时间为![]() ,
,
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
(2)∵B,D的坐标分别为:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理有:![]() ,
,
当![]() 为等腰三角形时,
为等腰三角形时,
①如图所示,当![]() 时,
时,
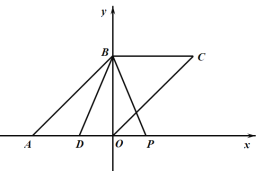
![]() ,
,
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
∴![]()
②如图所示,当![]() 时,
时,
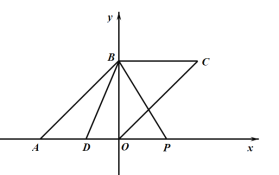
∵![]() ,
,![]()
∴![]() ,
,
∴![]()
③如图所示,当![]() 时,
时,

设P点坐标为:(![]() ,0)
,0)
则有:![]() ,
,![]() ,
,
∴![]() ,解之得:
,解之得:![]()
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
∴![]()
综上所述,当![]() 为1,
为1,![]() ,4时,
,4时,![]() 为等腰三角形;
为等腰三角形;
(3)答:存在![]() ,使得
,使得![]() 。
。
证明:∵A,B两点坐标分别为:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]()
∴![]()
即有:![]() ,
,
如图示,过D点作![]() 交BP于点F,
交BP于点F,

∵![]() ,
,
∴![]() ,
,
设![]() ,根据勾股定理有:
,根据勾股定理有:![]() ,
,
并且![]() ,
,
则:![]()
∴![]() ,
,
化简得:![]() ,
,
解之得:![]() (取正值),
(取正值),
即![]()
∴![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点F,B为圆心大于![]() FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )
FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )

A.12B.20C.24D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
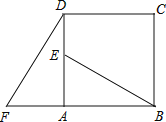
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)
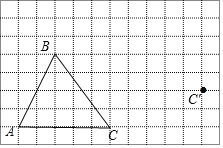
(1)画出平移后的△A′B′C′.
(2)画出AB边上的中线线CD;
(3)在整个平移过程中,线段BC扫过的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置。如图所示,
现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.
(1)画出△EDF;
(2)线段BD与AE有何关系? ____________;
(3)连接CD、BD,则四边形ABDC的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,如图∠BAC=90°,BD平分∠ABC,点E在BC上,DE∥AB,点F在BC上,连结AF,∠C=36°.
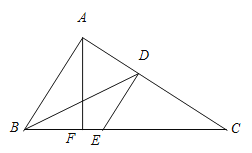
(1)求∠BDE的度数;
(2)若∠BAF∶∠CAF=2∶3,求证:AF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州中学在“读书日”期间购进一批图书,需要用大小两种规格的纸箱来装运。2个大纸箱和3个小纸箱一次可以装155本书,5个大纸箱和6个小纸箱一次可以装350本书.
(1)一个大纸箱和一个小纸箱分别可以装多少本书?
(2)如果一共购入800本书,分别需要用多少个大,小纸箱?请直接写出所有装书方案(两种纸箱都需要用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)
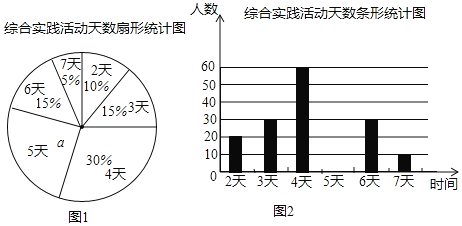
请你根据图中提供的信息,回答下列问题:
(1)扇形统计图中a的值为 ,“活动时间为4天”的扇形所对圆心角的度数为 °,该校初一学生的总人数为 ;
(2)补全频数分布直方图;
(3)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com