

分析 (1)先利用D等级的人数除以它占的百分比得到调查的总人数,然后用360°乘以C等级所占的百分比即可得到C等级对应扇形的圆心角的度数;
(2)A等级的人数为4人,假设小明用A表示,其他三人分别用B、C、D表示,利用画树状图展示所有12种等可能的结果数,再找出小明参加市演讲比赛的结果数,然后根据概率公式求解.
解答 解:(1)12÷30%=40,即调查的总人数为40人,
所以C等级对应扇形的圆心角=360°×$\frac{16}{40}$=144°,
故答案为144;
(2)A等级的人数为4人,假设小明用A表示,其他三人分别用B、C、D表示,
画树状图为:
共有12种等可能的结果数,小明参加市演讲比赛的结果数为6,
所以小明参加市演讲比赛的概率=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
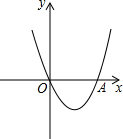 如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.
如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
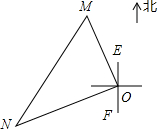 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( )
一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
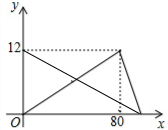 完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题:
完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
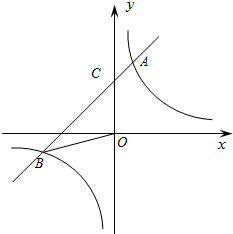 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
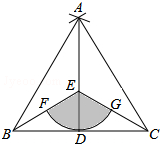 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com