
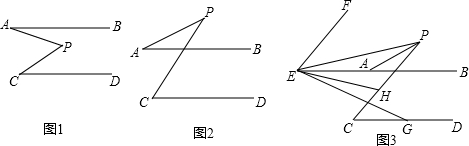
| 1 |
| 2 |
| 1 |
| 2 |
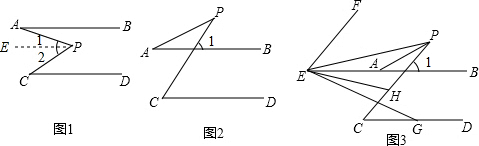 解:(1)∠P=∠A+∠C.
解:(1)∠P=∠A+∠C.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米.
一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米.查看答案和解析>>
科目:初中数学 来源: 题型:
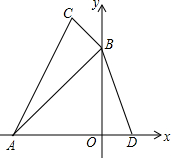 如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:
如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:查看答案和解析>>
科目:初中数学 来源: 题型:
 在一张城市地图上,有学校、医院、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏西75°方向,你能确定图书馆的位置吗?
在一张城市地图上,有学校、医院、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏西75°方向,你能确定图书馆的位置吗?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com