
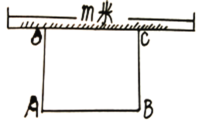
【题目】为配合我市“创建全国文明城市”某单位计划在一块矩形空地上修建绿色植物园(如图所示),其中边靠墙(墙长为![]() 米),另外三边用总长36米的材料围成.若
米),另外三边用总长36米的材料围成.若![]() 米,矩形
米,矩形![]() 的面积为
的面积为![]() 平方米.
平方米.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若矩形面积为160平方米,求![]() 的长.
的长.
(3)在(2)的前提下,墙长![]() 米对
米对![]() 的长有影响吗?请详细说明.
的长有影响吗?请详细说明.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
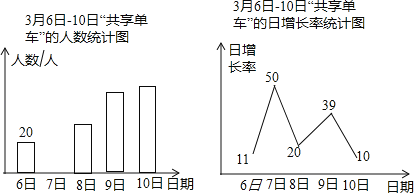
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
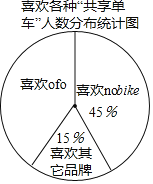
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究.
如图1,抛物线y=![]() x2﹣
x2﹣![]() x﹣2与x轴交于A,B两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
x﹣2与x轴交于A,B两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
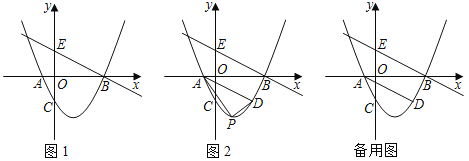
(1)求A,B,C三点的坐标及直线BE的解析式.
(2)如图2,过点A作BE的平行线交抛物线于点D,点P是抛物线上位于线段AD下方的一个动点,连接PA,PD,求OAPD面积的最大值.
(3)若(2)中的点P为抛物线上一动点,在x轴上是否存在点Q,使得以A,D,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC 内接于⊙O,过点 A 作⊙O 的切线交 CB 的延长线于点 P,且∠PAB=45°.
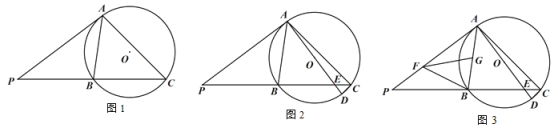
(1)如图 1,求∠ACB 的度数;
(2)如图 2,AD 是⊙O 的直径,AD 交 BC 于点 E,连接 CD,求证:AC CD ![]() ;
;
(3)如图 3 ,在(2)的条件下,当 BC 4![]() CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
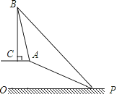
【题目】已知,如图,在笔山银子岩坡顶![]() 处的同一水平面上有一座移动信号发射塔
处的同一水平面上有一座移动信号发射塔![]() ,
,
笔山职中数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 移动信号发射塔
移动信号发射塔![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户今年1月初以20000元/亩的价格承包了10亩地用来种植某农作物,已知若按传统种植,每月每亩能产出3000千克,每亩的种植费用为2500元;若按科学种植,每月每亩产量可增加![]() ,但种植费用会增加2000元/亩,且前期需要再投入25万元,花费4个月的时间进行生长环境的改善,改善期间无法种植.已知每千克农作物市场售价为3元,每月底一次性全部出售,假设前
,但种植费用会增加2000元/亩,且前期需要再投入25万元,花费4个月的时间进行生长环境的改善,改善期间无法种植.已知每千克农作物市场售价为3元,每月底一次性全部出售,假设前![]() 个月销售总额为
个月销售总额为![]() (万元).
(万元).
(1)当![]() 时,分别求出两种种植方法下的销售总额
时,分别求出两种种植方法下的销售总额![]() ;
;
(2)问:若该农户选择科学种植,几个月后能够收回成本?
(3)在(2)的条件下,假如从2019年1月初算起,那么至少要到何时,该农户获得的总利润能够超过传统种植同样时间内所获得的总利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再解答问题.
恒等变形,是代数式求值的一个很重要的方法,利用恒等变形,可以把无理数运算转化为有理数运算,可以把次数较高的代数式转化为次数较低的代数式.如当x=![]() 时,求
时,求![]() ﹣x2﹣x+2的值,为解答这题,若直接把x=
﹣x2﹣x+2的值,为解答这题,若直接把x=![]() 代入所求的式中,进行计算,显然很麻烦.我们可以通过恒等变形,对本题进行解答.
代入所求的式中,进行计算,显然很麻烦.我们可以通过恒等变形,对本题进行解答.
方法一 将条件变形.因x=![]() ,得x﹣1=
,得x﹣1=![]() .再把所求的代数式变形为关于(x﹣1)的表达式.
.再把所求的代数式变形为关于(x﹣1)的表达式.
原式=![]() (x3﹣2x2﹣2x)+2
(x3﹣2x2﹣2x)+2
=![]() [x2(x﹣1)﹣x(x﹣1)﹣3x]+2
[x2(x﹣1)﹣x(x﹣1)﹣3x]+2
=![]() [x(x﹣1)2﹣3x]+2
[x(x﹣1)2﹣3x]+2
=![]() (3x﹣3x)+2
(3x﹣3x)+2
=2
方法二 先将条件化成整式,再把等式两边同时平方,把无理数运算转化为有理数运算.由x﹣1=![]() ,可得x2﹣2x﹣2=0,即,x2﹣2x=2,x2=2x+2.
,可得x2﹣2x﹣2=0,即,x2﹣2x=2,x2=2x+2.
原式=![]() x(2x+2)﹣x2﹣x+2
x(2x+2)﹣x2﹣x+2
=x2+x﹣x2﹣x+2
=2
请参以上的解决问题的思路和方法,解决以下问题:
(1)若a2﹣3a+1=0,求2a3﹣5a2﹣3+![]() 的值;
的值;
(2)已知x=2+![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com