Question

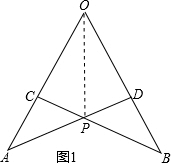
（1）[问题探究]在数学活动课上，老师给同学们提出了这样一个问题：如图1，已知OA=OB，OC=OD，AD和BC相交于点P，如果连接OP，那么OP平分∠AOB吗？
小颖同学认为OP平分∠AOB是正确的，并提出可以通过证明三次三角形全等来解决这个问题，
她的证明过程如下：
证明：在△AOD和△BOC中

OA=OB(已知) ∠O=∠O(公共角) OC=OD(已知)

∴△AOD≌△BOC（SAS）
∴∠A=∠B（全等三角形的对应角相等）
…
请你按照小颖的思路完成剩下的证明过程．
（2）[结论应用]由第（1）题中的结论，你能想到不同于平时课本中用尺规作角平分线的另一种方法吗？试在图2中，利用直尺和圆规，用不同于平时课本中的方法作出∠MON的平分线．
（保留作图痕迹，不写作法）

Answer 1

考点：全等三角形的判定与性质,作图—基本作图

专题：

分析：（1）根据AAS证明△APC≌△BPD，再由SSS证明△AOP≌△BOP，从而得出OP平分∠AOB；
（2）用尺规作图法作角平分线即可．

解答：证明：（1）∵OA=OB，OC=OD，
∴AC=BD，
在△APC和△BPD中，

∠A=∠B ∠APC=∠BPD AC=BD

，
∴△APC≌△BPD（AAS），
∴PA=PB，
连接OP，在△AOP和△BOP中，

PA=PB OA=OB OP=OP

，
∴△AOP≌△BOP（SSS），
∴∠AOP=∠BOP，
即OP平分∠AOB；
（2）以O为圆心，一定长为半径画弧与角两边OM、ON分别交于点A、B，再以O圆心，一定长为半径画弧与角两边OM、ON分别交于点C、D，且OC＜OA．连结BC、AD交于点P，连结OP，OP即为∠MON的平分线．

点评：本题考查了全等三角形的判定和性质，判断两个三角形全等的方法：SSS，SAS，ASA，AAS，还有直角三角形的判定定理：HL．