【题目】等腰三角形边长分别为
，
，且是关于
的一元二次方程
的两根，则
的值为__________；
【答案】10或6
【解析】
根据等腰三角形的性质可得出a=b或a=5或b=5，结合一元二次方程的解的意义即可得出关于n的一元一次方程，解之即可得出结论．
∵三角形是等腰三角形，
∴①a=b，②a=5或b=5两种情况，
①当a=b时，方程x2-6x+n-1=0有两个相等的实数根，
∴△=（-6）2-4（n-1）=0
解得：n=10，
②当a=5，或b=5时，
∵a，b是关于x的一元二次方程x2-6x+n-1=0的两根，
∴x=5，
把x=5代入x2-6x+n-1=0得，52-6×5+n-1=0，
解得：n=6，
当n=6时，原方程为x2-6x+5=0，
解得，x1=1，x2=5，
所以等腰三角形三边长为：5，5，1能组成三角形.
故答案为：10或6.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在
ABC中，过点C作CD//AB，E是AC的中点，连接DE并延长，交AB于点F，交CB的延长线于点G．连接AD、CF．
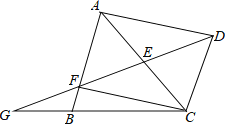
(1)求证：四边形AFCD是平行四边形；
(2)若GB＝3，BC＝6，BF＝1，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，抛物线y＝x2的图象如图所示．已知A点坐标为（1，1），过点A作AA1∥x轴交抛物线于点A1，过点A1作A1A2∥OA交抛物线于点A2，过点A2作A2A3∥x轴交抛物线于点A3，过点A3作A3A4∥OA交抛物线于点A4……，依次进行下去，则点A2019的坐标为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．
（1）若△BPQ与△ABC相似，求t的值；
（2）连接AQ、CP，若AQ⊥CP，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把抛物线y=
x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y=x2交于点Q，则图中阴影部分的面积为 ▲ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】新华商场为迎接家电下乡活动销售某种冰箱，每台进价为2500元，市场调研表明；当销售价定为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台，商场要想使这种冰箱的销售利润平均每天达到5000元，每台冰箱的定价应为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：如果两个正数a，b，即a＞0，b＞0，有下面的不等式：
，当且仅当a＝b时取到等号我们把
叫做正数a，b的算术平均数，把
叫做正数a，b的几何平均数，于是上述不等式可表述为：两个正数的算术平均数不小于（即大于或等于）它们的几何平均数．它在数学中有广泛的应用，是解决最值问题的有力工具．
初步探究：（1）已知x＞0，求函数y＝x+
的最小值．
问题迁移：（2）学校准备以围墙一面为斜边，用栅栏围成一个面积为100m2的直角三角形，作为英语角，直角三角形的两直角边各为多少时，所用栅栏最短？
创新应用：（3）如图，在直角坐标系中，直线AB经点P（3，4），与坐标轴正半轴相交于A，B两点，当△AOB的面积最小时，求△AOB的内切圆的半径．
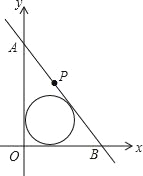
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．
（1）求证：△ABM∽△EFA；
（2）若AB=12，BM=5，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价
(单位:万元)成一次函数关系.
(1)求年销售量
与销售单价的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com