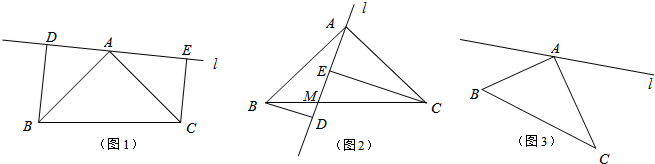
��ͼ1����Rt��ACB�У���BAC=90�㣬AB=AC���ֱ��B��C����������A��ֱ��l�Ĵ��ߣ�����ΪD��E��
��1����ͼ1����D��E������ֱ��BC��ͬ��ʱ�����룬BD��CE��DE�����߶���������������ϵ����˵�����ɣ�
��2����ͼ2����D��E������ֱ��BC������ʱ��BD��CE��DE�����߶ε�������ϵΪ
��
��3����ͼ2����ֱ��AD���سɵ��߶�AE��EM��MD�ij��ȷֱ���a��b��c����S
��ABM=S
1��S
��ACM=S
2����S
2-S
1��ֵ�����ú���a��b��c�Ĵ���ʽ��ʾ��
��4����ͼ3����BAC=90�㣬AB=22��AC=28����P��B�������B��A��C·�����յ�C�˶�����Q��C�������C��A��B·�����յ�B�˶�����P��Q�ֱ���ÿ��2��3����λ���ٶ�ͬʱ��ʼ�˶���ֻҪ��һ�㵽����Ӧ���յ�ʱ����ͬʱֹͣ�˶������˶������У��ֱ��P��Q��PF��l��F��QG��l��G���ʣ���P�˶�������ʱ����PFA���QAGȫ�ȣ���ֱ��д��������ɣ�





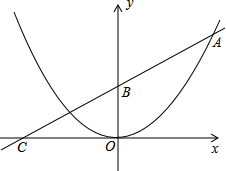 ��ͼ��֪���κ���ͼ��Ķ���Ϊԭ�㣬ֱ��y=
��ͼ��֪���κ���ͼ��Ķ���Ϊԭ�㣬ֱ��y=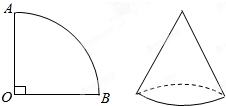 ��ͼ����֪����OAB��Բ�Ľ�Ϊ90�㣬�뾶Ϊ4���ף���������ξ��ɵ�Բ�IJ��棬���ԲԲ�IJ������Բ�ĸߣ�
��ͼ����֪����OAB��Բ�Ľ�Ϊ90�㣬�뾶Ϊ4���ף���������ξ��ɵ�Բ�IJ��棬���ԲԲ�IJ������Բ�ĸߣ�